
【题目】(1)命题“直角三角形的两个锐角互余”的条件是__________,结论是______________ ;它的逆命题是__________________.
(2)上题填的逆命题是真命题还是假命题?如果是真命题请给出证明,如果是假命题请举出反例.
【答案】(1)直角三角形的两个锐角;这两个锐角互余;有两个内角互余的三角形是直角三角形.(2)是真命题
【解析】
(1)命题有条件和结论两部分组成,条件是已知的,结论是结果,然后将命题的结论与条件互换即得到其逆命题;
(2)首先判断其是真命题,然后画出图形,写出证明过程.
解:(1)“直角三角形的两个锐角互余”的条件是直角三角形的两个锐角,结论是这两个锐角互余,逆命题是有两个内角互余的三角形是直角三角形.
故答案为直角三角形的两个锐角;这两个锐角互余;有两个内角互余的三角形是直角三角形.
(2)是真命题,证明如下:
解:如图所示:

∵在△ABC,∠A+∠B=90°,
∴∠C=180°-(∠A+∠B)=180°=90°,
∴△ABC是直角三角形.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两城相距1000千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为
千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为![]() (小时)
(小时)
(1)当![]() 时,客车与乙城的距离为 千米(用含
时,客车与乙城的距离为 千米(用含![]() 的代数式表示)
的代数式表示)
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
①求客车与出租车相距100千米时客车的行驶时间;(列方程解答)
②已知客车与出租车在甲、乙之间的服务站![]() 处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在![]() 处换成客车返回乙城.
处换成客车返回乙城.
是通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年4月8日—11日,博鳌亚洲论坛2018年年会在海南省博鳌镇召开.本届博鳌亚洲论坛的主题为“开放创新的亚洲,繁荣发展的世界”.围绕这一主题,年会设置了“全球化与一带一路”“开放的亚洲”“创新”“改革再出发”四大板块,展开60多场正式讨论.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,根据该程序的指令,首先输入![]() 的值为1,则输出的值为4,记作第一次操作;将第一次的输出值再次输入,则输出的值为2,记作第二次操作:…,如此循环操作,则第2020次操作输出的值为________.
的值为1,则输出的值为4,记作第一次操作;将第一次的输出值再次输入,则输出的值为2,记作第二次操作:…,如此循环操作,则第2020次操作输出的值为________.
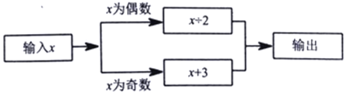
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]()
![]() 的取值范围.
的取值范围.
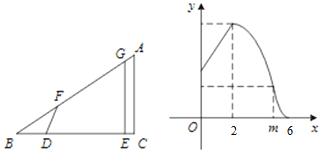
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com