
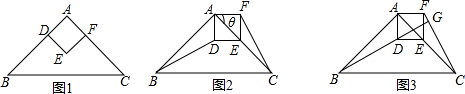
分析 (1)△ABC是等腰直角三角形,四边形ADEF是正方形,易证得△BAD≌△CAF,根据全等三角形的对应边相等,即可证得BD=CF;
(2)①由△BAD≌△CAF,可得∠ABM=∠GCM,又由对顶角相等,易证得△BMA∽△CMG,根据相似三角形的对应角相等,可得BGC=∠BAC=90°,即可证得BD⊥CF;
②首先过点F作FN⊥AC于点N,利用勾股定理即可求得AE,BC的长,继而求得AN,CN的长,又由等角的三角函数值相等,可求得AM=$\frac{1}{3}$AB=$\frac{4}{3}$,然后利用△BMA∽△CMG,求得CG的长,再由勾股定理即可求得线段BG的长.
解答 解:(1)BD=CF,理由如下:
∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC-∠DAC,∠CAF=∠DAF-∠DAC,
∴∠BAD=∠CAF,
在△BAD与△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴BD=CF;
(2)①BD⊥CF,证明:设BG交AC于点M,
∵△BAD≌△CAF(已证),
∴∠ABM=∠GCM,
∵∠BMA=∠CMG1,
∴△BMA∽△CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF;
②过点F作FN⊥AC于点N,如图: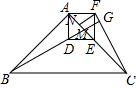
∵在正方形ADEF中,AD=DE=$\sqrt{2}$,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}=\sqrt{{\sqrt{2}}^{2}+{\sqrt{2}}^{2}}=2$,
∴AN=AN=$\frac{1}{2}$AE=1,
∵在等腰直角△ABC中,AB=4,
∴CN=AC-AN=3,BC=$\sqrt{A{B}^{2}+A{C}^{2}}=\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$,
∴在RT△FCN中,tan∠FCN=$\frac{FN}{CN}=\frac{1}{3}$,
在RT△ABM中,tan∠FCN=tan∠ABM=$\frac{AM}{AB}=\frac{1}{3}$,
∴AM=$\frac{1}{3}AB=\frac{4}{3}$,
∴CM=AC-AM=$4-\frac{4}{3}=\frac{8}{3}$,BM=$\sqrt{A{B}^{2}+A{M}^{2}}=\sqrt{{4}^{2}+(\frac{4}{3})^{2}}=\frac{4\sqrt{10}}{3}$,
∵△BMA∽△CMG,
∴$\frac{BM}{BA}=\frac{CM}{CG}$,即$\frac{\frac{4\sqrt{10}}{3}}{4}=\frac{\frac{8}{3}}{CG}$,
∴$CG=\frac{4\sqrt{10}}{5}$,
∴在RT△BGC中,BG=$\sqrt{B{C}^{2}-C{G}^{2}}=\sqrt{(4\sqrt{2})^{2}-(\frac{4\sqrt{10}}{5})^{2}}=\frac{8\sqrt{10}}{5}$.
点评 此题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质、矩形的性质、勾股定理以及三角函数等知识.此题综合性很强,难度较大,注意数形结合思想的应用,注意辅助线的作法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4x+4 | B. | -4x-2 | C. | -x+1 | D. | -2x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30.07×104 | B. | 3.007×105 | C. | 300.7×103 | D. | 0.3007×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com