
 如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.
如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
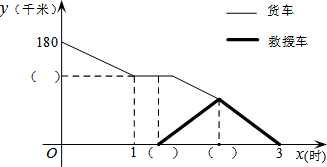 甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计).
甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
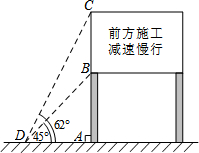 进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com