
【题目】如图,在△ABC中,∠A=∠C,将△ABC绕点B顺时针旋转![]() 度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=
度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=![]() ,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是___________________(写出正确结论的序号).
,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是___________________(写出正确结论的序号).

【答案】①②⑤
【解析】
①两个不同的三角形中有两个角相等,那么第三个角也相等;
②根据ASA进而得出△A1BF≌△CBE,即可得出A1E=CF;
③∠CDF=α,而∠C与顺时针旋转的度数不一定相等,所以DF与FC不一定相等;
④AE不一定等于CD,则AD不一定等于CE,
⑤用角角边可证明△A1BF≌△CBE后可得A1F=CE.
∵△ABC绕点B顺时针旋转α度,得到△A1BC1,
∴∠CBC1=α,∠C=∠C1,
∵∠BFC1=∠DFC,
∴∠CDF=∠CBC1=α,故①正确,
∵AB=BC,
∴∠A=∠C,
∴∠C=∠A1
在△A1BF和△CBE中,
∠C=∠A1,A1B=BC,∠A1BF=∠CBE,
∴△A1BF≌△CBE,
∴BE=BF,A1F=CE,故⑤正确,
∵A1B=BC,
∴A1B-BE=BC-BF,即A1E=CF,故②正确,
∵∠CDF=α,α是可变化的角,∠C是固定角,
∴∠CDF不一定等于∠C,
∴DF不一定等于CF,故③错误,
∵AE不一定等于CD,
∴AD不一定等于CE,故④错误.
综上所述:①②⑤正确,
故选C.


科目:初中数学 来源: 题型:
【题目】如图:在Rt△ABC中,∠C=90°,AC=BC,BE平分∠ABC交AC于点E,点D在BE的延长线上,AD⊥BE。
(1)求证:∠DAE+∠ABE=45°
(2)若BE=6,求AD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x满足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
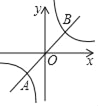
【题目】函数y=x的图象与函数y=![]() 的图象在第一象限内交于点A、B(2,m)两点.
的图象在第一象限内交于点A、B(2,m)两点.
(1)请求出函数y=![]() 的解析式;
的解析式;
(2)请根据图象判断当一次函数的值大于反比例函数的值时x的取值范围;
(3)点C是函数y=![]() 在第一象限图象上的一个动点,当OBC的面积为3时,请求出点C的坐标.
在第一象限图象上的一个动点,当OBC的面积为3时,请求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点
过点![]() 和
和![]() ,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作
,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作![]() ,且
,且![]() ,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
![]() 求抛物线解析式;
求抛物线解析式;
![]() 当点D落在抛物线上时,求点P的坐标;
当点D落在抛物线上时,求点P的坐标;
![]() 若以A、B、D为顶点的三角形与
若以A、B、D为顶点的三角形与![]() 相似,请直接写出此时t的值.
相似,请直接写出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 | 4 | 6 | 6 | 4 |
|
小聪观察上表,得出下面结论:![]() 抛物线与x轴的一个交点为
抛物线与x轴的一个交点为![]() ;
;![]() 函数
函数![]() 的最大值为6;
的最大值为6;![]() 抛物线的对称轴是
抛物线的对称轴是![]() ;
;![]() 在对称轴左侧,y随x增大而增大
在对称轴左侧,y随x增大而增大![]() 其中正确有
其中正确有![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备把240吨白砂糖运往![]() 、
、![]() 两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见下表:
两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见下表:
载重量 | 运往 | 运往 | |
大车 | 15吨/辆 | 650元/辆 | 700元/辆 |
小车 | 10吨/辆 | 400元/辆 | 500元/辆 |
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往![]() 地,其中大车有
地,其中大车有![]() 辆,其余货车前往
辆,其余货车前往![]() 地,且运往
地,且运往![]() 地的白砂糖不少于130吨.
地的白砂糖不少于130吨.
①![]() 的取值范围;
的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com