
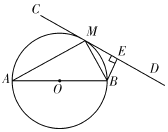
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE丄CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.
【答案】(1)见解析;(2)8
【解析】
试题
(1)如图,连接OM,由CD切⊙O于点M证得∠BME和∠OMB互余;由AB是⊙O直径证得∠AMO和∠OMB互余;从而可得∠BME=∠AMO,再证∠AMO=∠BAM即可得到结论;
(2)首先证∠BEM=∠BMA=90°,结合(1)中所得∠BME=∠BAM可证得△BEM∽△BMA,由此可得BE:BM=BM:AB,即BM2=BE·AB;
(3)由∠BME=∠BAM和sin∠BAM=![]() ,可得sin∠BME=
,可得sin∠BME=![]() ,从而在Rt△BME中,可得BM=
,从而在Rt△BME中,可得BM=![]() BE=6;然后在Rt△ABM中,由sin∠BAM=
BE=6;然后在Rt△ABM中,由sin∠BAM=![]() ,可得AB=
,可得AB=![]() BM=10,最后在Rt△ABM中由勾股定理可求得AM的长.
BM=10,最后在Rt△ABM中由勾股定理可求得AM的长.
试题解析:
(1)如图,连接OM.
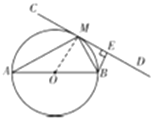
∵直线CD切⊙O于点M,
∴∠OMD=90°
∴∠BME+∠OMB=90°.
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°.
∴∠BME=∠AMO.
∵OA=OM,
∴∠MAB=∠AMO.
∴∠BMA=∠MAB.
(2)由(1)知∠BME=∠MAB.
∵BE![]() CD,
CD,
∴∠BEM=∠AMB=90°.
∴△BME∽△BAM.
∴![]() ,
,
∴BM2=BE·AB.
(3)由(1)知∠BME=∠MAB.
∵sin∠BAM=![]() ,
,
∴sin∠BME=![]() .
.
在Rt△BEM中,BE=![]() ,
,
∴sin∠BAM=![]() =
=![]() ,
,
∴BM=![]() BE=6.
BE=6.
在Rt△ABM中, sin∠BAM=![]() ,
,
∴sin∠BAM=![]() =
=![]() ,
,
∴AB=![]() BM=10.
BM=10.
在Rt△ABM中,根据勾股定理,得AM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: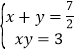 ,消去y化简得:2x2﹣7x+6=0,
,消去y化简得:2x2﹣7x+6=0,
∵△=49﹣48>0,
∴x1=_____,x2=_______,
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() .与
.与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上.
上.
(1)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(2)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为
的增大而增大的部分为![]() ,直线
,直线![]() 向下平移
向下平移![]() 个单位,当平移后的直线与
个单位,当平移后的直线与![]() 有公共点时,求
有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
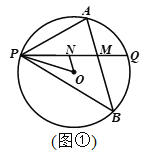
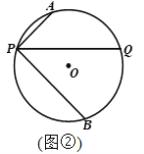
【题目】已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径;
时,求⊙O的半径;
(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店以每件40元的价格购进一批衬衫,在试销过程中发现:每月销售量y(件)与销售单价x(x为正整数)(元)之间符合一次函数关系,当销售单价为55元时,月销售量为140件;当销售单价
为70元时,月销售量为80件.
(1)求y与x的函数关系式;
(2)如果每销售一件衬衫需支出各种费用1元,设服装店每月销售该种衬衫获利为w元,求w与x之间的函数关系式,并求出销售单价定为多少元时,商场获利最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com