
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D.
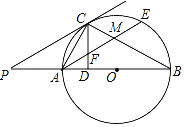
(1)求证:∠PCA=∠ABC;
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,交BC于点M,若∠CAB=2∠B,CF=![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)如图,连接OC,利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB,利用等量代换可得∠PCA=∠ABC.
(2)先求出△OCA是等边三角形,在利用三角形的等边对等角定理求出FA=FC和CF=FM,然后分别求出AM、AC、MO、CD的值,分别求出![]() 、
、![]() 、
、![]() 的值,利用
的值,利用![]() ,然后通过计算即可解答.
,然后通过计算即可解答.
解:(1)证明:连接OC,如图,
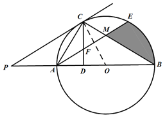
∵PC切⊙O于点C,∴OC⊥PC,
∴∠PCA+∠ACO=90,
∵AB是⊙O的直径,∴∠ACB=∠ACO+OCB=90
∴∠PCA=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠PCA=∠ABC;
(2)连接OE,如图,
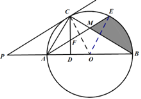
∵△ACB中,∠ACB=90,∠CAB=2∠B,
∴∠B=30,∠CAB=60,∴△OCA是等边三角形,
∵CD⊥AB,∴∠ACD+∠CAD=∠CAD+∠ABC=90,
∴∠ACD=∠B=30,
∵PC∥AE,∴∠PCA=∠CAE=30,∴FC=FA,
同理,CF=FM,∴AM=2CF=![]() ,
,
Rt△ACM中,易得AC=![]() ×
×![]() =3=OC,
=3=OC,
∵∠B=∠CAE=30,∴∠AOC=∠COE=60,
∴∠EOB=60,∴∠EAB=∠ABC=30,∴MA=MB,
连接OM,EG⊥AB交AB于G点,如图所示,
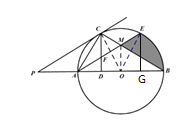
∵OA=OB,∴MO⊥AB,∴MO=OA×tan30=![]() ,
,
∵△CDO≌△EDO(AAS),
∴EG=CD=AC×sin60=![]() ,
,
∴![]() ,
,
同样,易求![]() ,
,
![]()
∴![]() =
=![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
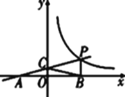
(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
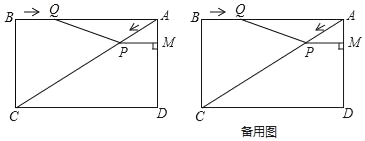
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
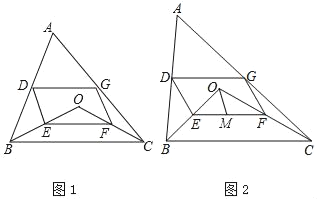
【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E、F分别在CD、AD上,CE=DF,BE、CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为3:4,则△BCG的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
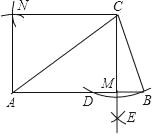
【题目】如图,已知等腰△ABC中,AB=AC.以C为圆心,CB的长为半径作弧,交AB于点D.分别以B、D为圆心,大于![]() BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
(1)求证:AN⊥CN
(2)若AB=5,tanB=3,求四边形AMCN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
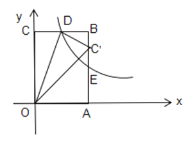
【题目】如图,平面直角坐标系中,矩形ABCD与双曲线![]() 交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
A. 4B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
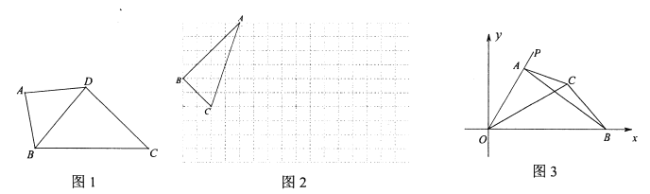
(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(2)如图2,已知格点![]() ,请你在正方形网格中画出所有的格点四边形
,请你在正方形网格中画出所有的格点四边形![]() ,使四边形
,使四边形![]() 是以
是以![]() 为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
(3)如图3,四边形![]() 中,点
中,点![]() 在射线
在射线![]() :
:![]() 上,点
上,点![]() 在
在![]() 轴正半轴上,对角线
轴正半轴上,对角线![]() 平分
平分![]() ,连接
,连接![]() .若
.若![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com