
����Ŀ����ͼ1����ֱ������ϵxoy�У�O������ԭ�㣬��A��x�������ϣ�OA=12 ![]() cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2
cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2 ![]() cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6��s��
cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊt��0��t��6��s�� 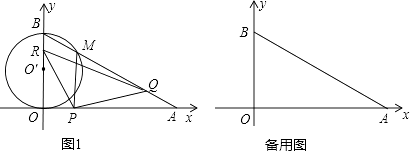
��1�����OAB�Ķ�����
��2����OBΪֱ���ġ�O����AB���ڵ�M����tΪ��ֵʱ��PM���O�����У�
��3���Ƿ���ڡ�RPQΪ���������Σ������ڣ���ֱ��д��tֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��Rt��AOB�У�
tan��OAB= ![]() =
= ![]() =
= ![]() ��
��
���OAB=30��
��2���⣺��ͼ������O��P��O��M��
��PM���O������ʱ���У�
��PMO��=��POO��=90�㣬
��PMO��ա�POO�䣮
�ɣ�1��֪��OBA=60�㣬
��O��M=O��B��
���O��BM�ǵȱ������Σ�
���BO��M=60�㣮
�ɵá�OO��P=��MO��P=60�㣮
��OP=OO��tan��OO��P
=6��tan60��=6 ![]() ��
��
�֡�OP=2 ![]() t��
t��
��2 ![]() t=6
t=6 ![]() ��t=3��
��t=3��
����t=3ʱ��PM���O������
��3���⣺���ڡ�RPQΪ���������Σ�
�������£��������֪��PR2=16t2��48t��PQ2=52t2��288t��RQ2=28t2��240t+576��
����PR=RQʱ���ɵ�t=8��2 ![]() ��t=8+
��t=8+ ![]() ��ȥ����
��ȥ����
����PR=PQʱ���ɵ�t= ![]() ��
��
����RQ=PQʱ���ɵ�t=1+ ![]() ��t=1��
��t=1�� ![]() ��ȥ��
��ȥ��
���Ͽ�֪����t=8��2 ![]() ��
�� ![]() ��1+
��1+ ![]() ʱ����RPQΪ���������Σ�
ʱ����RPQΪ���������Σ�
����������1����Rt��OAB�У���֪��OA��OB�ij������������OAB������ֵ���ɴ˿ɵõ���OAB�Ķ�������2������O��M����PM���O������ʱ��PM��POͬΪ��O������ߣ���֤�á�OO��P�ա�MO��P�����OO��P=��MO��P���ڣ�1�����á�OBA=60�㣬����O��BM�ǵȱ������Σ��ɴ˿ɵõ���BO��M=��PO��M=��PO��O=60�㣻��Rt��OPO���У����ݡ�PO��O�Ķ�����OO��ij��������OP�ij�����֪��P����˶��ٶȣ����ɸ���ʱ��=·�̡��ٶ����t��ֵ����3�����ڡ�RPQΪ���������Σ����ڡ�QPQ�����͵ײ�ȷ������������ۣ���PR=RQ����PR=PQ����RQ=PQʱ�ֱ�������������tֵ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
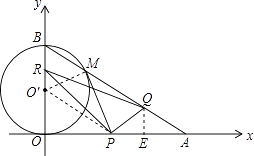
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=x2+mx+n������A��3��0����B��0����3������P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ��߽��������ڵ�M�����P�ĺ�����Ϊt��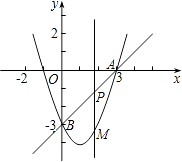
��1���ֱ����ֱ��AB�����������ߵĽ���ʽ��
��2������P�ڵ������ޣ�����AM��BM�����߶�PM�ʱ�����ABM�������
��3���Ƿ���������ĵ�P��ʹ���Ե�P��M��B��OΪ������ı���Ϊƽ���ı��Σ������ڣ��������P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������һ����P��������Χ3���ﴦ�а�����һ�ҿ�����9����/ʱ���ٶ��������У�����A�㴦���P�����ı�ƫ��60��ķ�������ʻ20���Ӻ���B���ֲ�õ���P�����ı�ƫ��45�㷽���ʿ��ֲ��ı䷽�����ǰ����������Σ�գ� 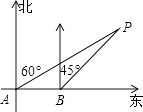
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=��x+4��ͼ���뷴����![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2������OA��OB�����AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ԲȦ�ֱ��ʾ�������Ϻ��������ϣ�����������ԲȦ�ڸ����������������������������ڸ��������ڣ��������������ڣ���������Ӧ�����������˵��������ԲȦ���ص����ֱ�ʾʲô���ļ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ƽ�Ƶ��ǣ� ��
A. С���˵��ݴ�һ¥����¥ B. �ӱ���ת��
C. һ������Ӹߴ��������� D. С�����������»�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ������C��DΪԲ�����㣬�һ�CB=��CD��CF��AB�ڵ�F��CE��AD���ӳ����ڵ�E�� 
��1����˵����DE=BF��
��2������DAB=60�㣬AB=6�����ACD�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com