
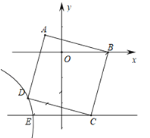
【题目】如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.已知DF:FA=1:2.
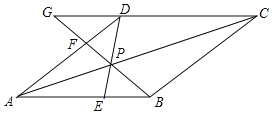
(1)求证:△APB≌△APD;
(2)当线段DP的长为6时,求线段FG的长;
(3)请直接写出![]() 的比值.
的比值.
【答案】(1)详见解析;(2)线段FG的长为5;(3)![]() .
.
【解析】
(1)由菱形的性质知∠BAP=∠DAP,AB=AD,再结合AP=AP即可证得△APB≌△APD;
(2)首先证明△AFP∽△CBP,得出![]() ,由
,由![]() 知
知![]() ,根据PB=PD知PF=
,根据PB=PD知PF=![]() PD,结合DP=6可得FB=10,再证△DFG∽△AFB得
PD,结合DP=6可得FB=10,再证△DFG∽△AFB得![]() ,从而得出答案;
,从而得出答案;
(3)由△APF∽△CBP,且![]() 知
知![]() =(
=(![]() )2=
)2=![]() ,由S△ABC=S△ADC,S△ABP=S△ADP知S△PBC=S△PDC,即可得出答案.
,由S△ABC=S△ADC,S△ABP=S△ADP知S△PBC=S△PDC,即可得出答案.
解:(1)由菱形的性质知∠BAP=∠DAP,AB=AD,
在△APB和△APD中,
∵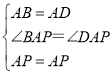 ,
,
∴△APB≌△APD(SAS);
(2)∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴△AFP∽△CBP,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]()
由(1)知PB=PD,
∴![]() .
.
∴PF=![]() PD,
PD,
当DP=6时,PF=![]() ×6=4,
×6=4,
∴FB=FP+PB=4+6=10.
∵DG∥AB,
∴△DFG∽△AFB.
∴![]() ,
,
∴FG=![]() ×10=5
×10=5
(3)由(2)知△APF∽△CBP,且![]()
∴![]() =(
=(![]() )2=
)2=![]() ,
,
又∵S△ABC=S△ADC,S△ABP=S△ADP,
∴S△PBC=S△PDC,
∴![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
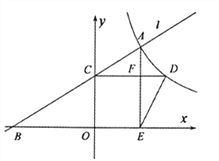
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合),且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.
(1)求证:△APQ≌△QCE;
(2)求∠QAE的度数;
(3)设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y![]() 上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
上,过点C作CE∥x轴交双曲线于点E,则CE的长为( )
A. 2.5B. 3C. 3.5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )

A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() .
.
把x=![]() 代入已知方程,得
代入已知方程,得![]() +
+![]() -1=0.
-1=0.
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为_________;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙)用60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com