
【题目】如图,△ABC中,∠ACB=90°,点E在BC上,以CE为直径的⊙O交AB于点F,AO∥EF
(1)求证:AB是⊙O的切线;
(2)如图2,连结CF交AO于点G,交AE于点P,若BE=2,BF=4,求![]() 的值.
的值.
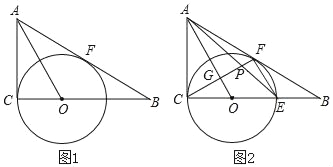
【答案】(1)证明见解析(2)2
【解析】
(1)连接OF,如图1,证明△AOC≌△AOF,根据全等三角形的性质可得∠AFO=∠ACO=90°,即可证得AB是⊙O的切线;
(2)如图2,在Rt△OFB中,设OE=OF=r,利用勾股定理求得r=3,从而得OB=5,设AC=AF=t,则AB=4+t,在Rt△ACB中,利用勾股定理求得t,即可得AC=6,从而可得AO长,然后证明△ACO∽△AGO,继而可推导得出AO=![]() AG,再证明△BEF∽△BOA,从而可推导得出
AG,再证明△BEF∽△BOA,从而可推导得出![]() ,再证明△PEF∽△PAG,根据相似三角形的性质即可求得
,再证明△PEF∽△PAG,根据相似三角形的性质即可求得![]() =2.
=2.
(1)连接OF,如图1,
∵OA∥EF,
∴∠1=∠3,∠2=∠4,
∵OE=OF,
∴∠3=∠4,
∴∠1=∠2,
在△AOC和△AOF中,
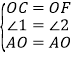 ,
,
∴△AOC≌△AOF,
∴∠ACO=∠AFO=90°,
∴OF⊥AB,
∴AB是⊙O的切线;
(2)如图2,在Rt△OFB中,设OE=OF=r,
∵OF2+BF2=OB2,
∴r2+42=(r+2)2,解得r=3,
∴OB=5,
设AC=AF=t,则AB=4+t,
在Rt△ACB中,t2+82=(t+4)2,解得t=6,
即AC=6,
∴AO=![]() ,
,
∵∠CAO=∠GAO,∠ACO=∠AGC=90°,
∴△ACO∽△AGO,
∴AC:AO=AG:AC,
∴AC2=AOAG,
∴AG=![]() ,
,
∴AO=![]() AG,
AG,
∵OA∥EF,
∴△BEF∽△BOA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵EF∥GA,
∴△PEF∽△PAG,
∴![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=4,则这两块直角三角板顶点A、A′之间的距离等于___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形纸片ABCD中,AB=3,AD=9,折叠纸片ABCD,使顶点C落在边AD上的点G处,折痕分别交边AD、BC于点E、F,则△GEF的面积最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
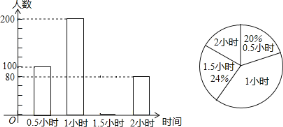
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12.在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,则CN=__________.
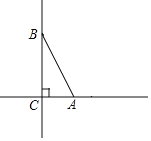
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com