
【题目】如图,已知在平行四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两点,则以下条件不能判断四边形
上的两点,则以下条件不能判断四边形![]() 是平行四边形的是( )
是平行四边形的是( )
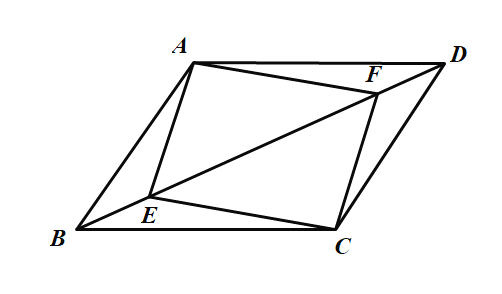
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】
连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解.
解:如图,连接AC与BD相交于O,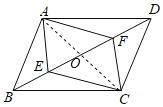
在ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、AF=EF无法证明得到OE=OF,故本选项正确.
B、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,则OB-BE=OD-DF,即OE=OF,故本选项错误;
C、若AF⊥CF,CE⊥AE,由直角三角形的性质可得OE=![]() AC=OF,故本选项错误;
AC=OF,故本选项错误;
D、若BE=DF,则OB-BE=OD-DF,即OE=OF,故本选项错误;
故选:A.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】小李在学校“青少年科技创新比赛”活动中,设计了一个沿直线轨道做匀速直线运动的模型.甲车从![]() 处出发向
处出发向![]() 处行驶,同时乙车从
处行驶,同时乙车从![]() 处出发向
处出发向![]() 处行驶.如图所示,线段
处行驶.如图所示,线段![]() 、
、![]() 分别表示甲车、乙车离
分别表示甲车、乙车离![]() 处的距离
处的距离![]() (米)与已用时间
(米)与已用时间![]() (分)之间的关系.试根据图象,解决以下问题:
(分)之间的关系.试根据图象,解决以下问题:
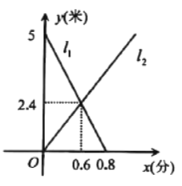
(1)填空:出发_________(分)后,甲车与乙车相遇,此时两车距离![]() 处________(米);
处________(米);
(2)求乙车行驶![]() (分)时与
(分)时与![]() 处的距离.
处的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家蓝莓采摘园的蓝莓品质相同,销售价格都是每千克30元,两家均推出了“周末”优惠方案.甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需要购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠.优惠期间,设某游客的蓝莓采摘量为![]() 千克,在甲采摘园所需总费用为
千克,在甲采摘园所需总费用为![]() 元,在乙采摘园所需总费用为
元,在乙采摘园所需总费用为![]() 元.
元.
(1)求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)该游客如何选择采摘园去采摘比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果m是从0,1,2,3四个数中任取的一个数,n是从0,1,2三个数中任取的一个数,那么关于x的一元二次方程x2-2mx+n2=0有实数根的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() ,
,![]() 为对角线
为对角线![]() 上的一点,连接
上的一点,连接![]() 和
和![]() .
.
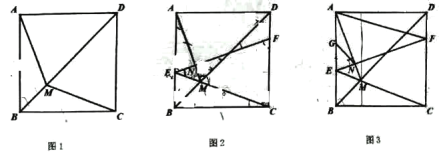
(1)求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点,且有
于点,且有![]() .
.
①判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
②如图3,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,当四边形
,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
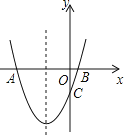
【题目】如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
(1)求抛物线的对称轴及k的值;
(2)求抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两。问:每头牛、每只羊各值金多少两?” 设每头牛值金 x 两,每只羊值金 y 两,则列方程组错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com