
 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
分析 由条件可以知道DE是△ABC的中位线,根据中位线的性质就可以求出$\frac{DE}{BC}=\frac{1}{2}$,再根据相似三角形的性质就可以得出结论.
解答 解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,$\frac{DE}{BC}=\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{1}{2})^{2}$,
∵△ADE的面积为4,
∴$\frac{4}{{S}_{△ABC}}=\frac{1}{4}$,
∴S△ABC=16.
故选:C.
点评 本题考查中位线的判定及性质的运用,相似三角形的判定及性质的运用,解答时证明△ADE∽△ABC是解答本题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
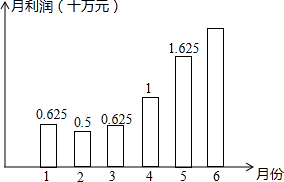 甲、乙两玩具厂从已有订单来看,两厂都预计自2011年起本厂的月利润y(十万元)与月份x之间满足一定的函数关系.甲厂预测的关系:y=$\frac{1}{8}$x2-x+2;乙厂则预测该厂的月利润与月份也满足二次函数关系,且图象形状与甲厂的相同.又知乙厂预测的该厂前几个月份的月利润如图所示,试根据上述信息解决下列问题:
甲、乙两玩具厂从已有订单来看,两厂都预计自2011年起本厂的月利润y(十万元)与月份x之间满足一定的函数关系.甲厂预测的关系:y=$\frac{1}{8}$x2-x+2;乙厂则预测该厂的月利润与月份也满足二次函数关系,且图象形状与甲厂的相同.又知乙厂预测的该厂前几个月份的月利润如图所示,试根据上述信息解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
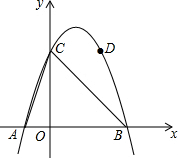 某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.
某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
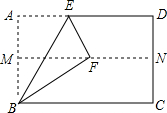 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 36° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com