
分析 先把解析式配成顶点式得到抛物线的顶点坐标为(-m,m2+4m+5),设抛物线与x轴两交点的坐标为(α,0),(β,0),利用抛物线与x轴的交点问题,可判断α、β为方程-x2-2mx+4m+5=0的两实数解,由根与系数的关系得到α+β=-2m,αβ=-(4m+5),利用代数式变形得到|α-β|=$\sqrt{(α+β)^{2}-4αβ}$=2$\sqrt{(m+1)^{2}+1}$,则根据三角形面积公式得到抛物线与x轴的两个交点和它的顶点所组成的三角形面积=$\frac{1}{2}$•(m2+4m+5)•2$\sqrt{(m+1)^{2}+1}$=[(m+1)2+1]•$\sqrt{(m+1)^{2}+1}$,利用二次函数性质得m=-1时,(m+1)2+1有最小值1,$\sqrt{(m+1)^{2}+1}$也有最小值1,于是得到三角形面积的最小值为1.
解答 解:y=-x2-2mx+4m+5=-(x+m)2+m2+4m+5,则抛物线的顶点坐标为(-m,m2+4m+5),
设抛物线与x轴两交点的坐标为(α,0),(β,0),则α、β为方程-x2-2mx+4m+5=0的两实数解,
所以α+β=-2m,αβ=-(4m+5),则|α-β|=$\sqrt{(α+β)^{2}-4αβ}$=$\sqrt{4{m}^{2}+4(4m+5)}$=2$\sqrt{(m+1)^{2}+1}$,
所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积=$\frac{1}{2}$•(m2+4m+5)•2$\sqrt{(m+1)^{2}+1}$=[(m+1)2+1]•$\sqrt{(m+1)^{2}+1}$,
因为m=-1时,(m+1)2+1有最小值1,$\sqrt{(m+1)^{2}+1}$也有最小值1,
所以抛物线与x轴的两个交点和它的顶点所组成的三角形面积的最小值为1.
故答案为-1,1.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
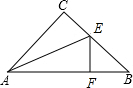 已知如图,∠C=90°,AE平分∠BAC交BC于E,EF⊥AB于F.
已知如图,∠C=90°,AE平分∠BAC交BC于E,EF⊥AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
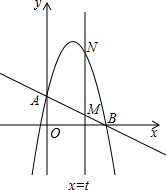 如图,一次函数y=-$\frac{1}{2}x+2$分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
如图,一次函数y=-$\frac{1}{2}x+2$分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
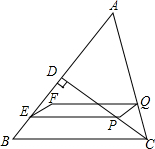 如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P、Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P、Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连结PQ.当点P、E不重合点P、Q不重合时,以线段PE∥BC,交AB于点E,连结PQ.当点P、E不重合且点P、Q不重合时,以线段PE、PQ为一组邻边作?PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).
如图,在△ABC中,AC=BC=5cm,AB=6cm,CD⊥AB于点D.动点P、Q同时从点C出发,点P沿线CD做依次匀速往返运动,回到点C停止;点Q沿折线CA-AD向终点D做匀速运动;点P、Q运动的速度都是5cm/s.过点P作PE∥BC,交AB于点E,连结PQ.当点P、E不重合点P、Q不重合时,以线段PE∥BC,交AB于点E,连结PQ.当点P、E不重合且点P、Q不重合时,以线段PE、PQ为一组邻边作?PEFQ.设点P运动的时间为t(s),?PEFQ与△ABC重叠部分的面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
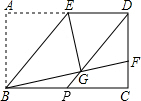 如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.
如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
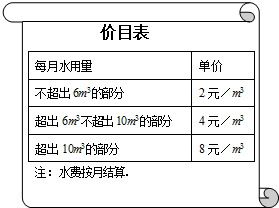 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.若某户居民1月份用水8m3,则应收水费:2×6+4×(8-6)=20元.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.若某户居民1月份用水8m3,则应收水费:2×6+4×(8-6)=20元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com