
【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]() ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1 , △OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2 , 记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3 , 记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016 , 记抛物线y2016与x轴的另一交点为A2016 , 顶点为P2016 . 若这2016条抛物线的顶点都在射线OP1上.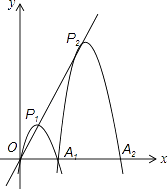
(1)①求△OP1A1的面积;②求a,b的值;
(2)求抛物线y2的解析式;
(3)请直接写出点A2016以及点P2016坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三点分别在CD、AD、BC上,如图所示.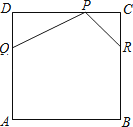
(1)当皮雕师傅切下△PDQ时,若DQ长度为x公分,请你以x表示此时△PDQ的面积.
(2)承(1),当x的值为多少时,五边形PQABR的面积最大?请完整说明你的理由并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上两点A,B对应的数分别是﹣1,3,点P为数轴上的一动点,其对应的数为x

(1)A、B两点的距离AB= ;
(2)在数轴上是否存在点P,使PA+PB=6?若存在,请求出x的值;若不存在,请说明理由.
(3)如图2,若点P以每秒1个单位的速度从点O出发向右运动,同时点A以每秒5个单位的速度向左运动,点B以每秒20个单位的速度向右运动,在运动的过程中,M、N分别是AP、OB的中点,问:![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.
上,AD// BC//y 轴.
(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;
(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;
(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2018的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com