
����Ŀ��ijʳƷ�ӹ�����Ҫһ��ʳƷ��װ�У���Ӧ���ְ�װ�������ַ����ɹ�ѡ��
����һ���Ӱ�װ�мӹ���ֱ�ӹ���������ķ�y1���װ����x������ͼ1��ʾ�ĺ�����ϵ��
���������������Լ��ӹ����������y2�������������ķ��ú�������װ�еķ��ã����װ����x������ͼ2��ʾ�ĺ�����ϵ������ͼ��ش��������⣺
��1������һ��ÿ����װ�еļ۸��Ƕ���Ԫ��
��2�����������������ķ����Ƕ���Ԫ������һ����װ�еķ����Ƕ���Ԫ��
��3����ֱ����y1��y2��x�ĺ�����ϵʽ��
��4��������Ǿ����ߣ�����ΪӦ��ѡ�����ַ�����ʡǮ����˵������

���𰸡�(1)��5Ԫ��(2)��20000Ԫ��2.5Ԫ��(3)��y1=5x��y2=2.5x+20000��(4)����x=8000ʱ�����ַ���ͬ��ʡǮ����x��8000ʱ��ѡ��һ����x��8000ʱ��ѡ����.
�����������������(1)������ͼһ�ó��𰸣�(2)������ͼ���ó��������ķ��úͺ��ӵĵ��ۣ�(3)�����ô���ϵ�����ֱ�������������Ľ���ʽ��(4)����������������ʱx��ֵ��Ȼ��ó���.
���������(1)��500��100=5�� ������һ�ĺ��ӵ���Ϊ5Ԫ��
(2)�����ݺ�����ͼ�����֪���������ķ���Ϊ20000Ԫ��
���ӵĵ���Ϊ��30000��20000����4000=2.5�� �ʺ��ӵĵ���Ϊ2.5Ԫ��
(3)����ͼ��һ�ĺ�������ʽΪ��y1=k1x�� ��ͼ��֪���������㣨100��500���� ��500=100k1��
���k1=5�� �������Ľ���ʽΪy1=5x��
��ͼ����ĺ�����ϵʽΪy2=k2x+b
��ͼ��֪��������ͼ���㣨0��20000���ͣ�4000��30000����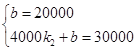 ��
��
��ã�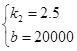 �� �������Ľ���ʽΪy2=2.5x+20000��
�� �������Ľ���ʽΪy2=2.5x+20000��
(4)����5x=2.5x+20000�� ���x=8000��
����x=8000ʱ�����ַ���ͬ��ʡǮ����x��8000ʱ��ѡ��һ����x��8000ʱ��ѡ������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1����ͼ1����֪��O�İ뾶��4����ABC�ڽ��ڡ�O��AC=4 ![]() ��
��
�����ABC�Ķ�����
����֪AP�ǡ�O�����ߣ���AP=4������PC���ж�ֱ��PC���O��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����֪ABCD�Ķ���A��B��D�ڡ�O�ϣ�����C�ڡ�O�ڣ��ӳ�BC����O�ڵ�E������DE����֤��DE=DC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��2��2����B��4��2����C��6��4������ԭ��OΪλ�����ģ�����ABC��СΪԭ����һ�룬���߶�AC���е�P�任���ڵ�һ����Ӧ�������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ��ѧУ�����ġ�ѹ��Ǯ��������г������飬�õ�һ��ѧ���������ݣ�
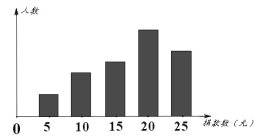
��ͼ�Ǹ����������ݻ��Ƶ�ͳ��ͼ��ͼ�д����ҳ����εĸ߶�֮��Ϊ2:4:5:8:6.��֪�˴ε����о��20Ԫ��25Ԫ��ѧ��һ��28��.
��1������һ�������˶���ѧ����
��2��д���������ݵ���λ����������
��3������У����2000��ѧ��������ȫУѧ����Լ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��DE��AC��DF��AC��DF���������������������ж� ��ABC�ա�DEF���ǣ� ��
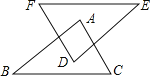
A. EF��BC B. AB��DE C. EF��BC D. ![]() B��
B��![]() E
E
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC
��1����ֱ�ߺ�Բ������ABC�ı�BC�ϵĸ�AD�������߶�AD����һ��E��ʹE��AB�ľ������ED����д������������ͼ�ۼ�����
��2����AB=AC=5��BC=6�����ED�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
��1��һ�����ӣ����װ���ӿ���װ18�������װ�����װ16�����ֹ��г��ӡ���400��������װ���������װ�������ӵ�2��������һ�£�װ���Ӻ�װ������Ӹ����ٸ���
��2��һȺС����һ��ƻ����ÿ��3����7����ÿ��4����3�������м���С��������ƻ����
��3��һ�ܷɻ�������֮����У�����Ϊ24ǧ��/ʱ��˳�������Ҫ2Сʱ50�֣���������Ҫ3Сʱ������ʱ�ɻ����ٶȺ�����֮��ĺ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̣��飩��Ӧ����
(1)ij��ѧ��֯��һѧ�����Σ�ԭ�ƻ�����45������������������15��û����λ��������ͬ��������60�����������45���������һ�����˳�����������ͳ�ǡ���������ʳ�һ�꼶�����Ƕ��٣�ԭ�ƻ�����45��������������
(2)�������㾭�����й��Ŵ���Ҫ����ѧ����������������Ȥ���ֲ������ɵ�������ʽ�����м��أ������мס��Ҷ��ˣ���Ǯ����֪���������а룬������ʮ�ˣ��ҵü�̫�룬������ʮ�ˣ��ʼס��Ҷ���ԭ��Ǯ�����Σ������ģ����ף������˸�������Ǯ������õ�������Ǯ��һ�룬��ô����Ǯ48�ģ�����ҵõ�������Ǯ��![]() ����ô��Ҳ����Ǯ48�ģ��ʼף��Ҷ���ԭ�����ж���Ǯ����
����ô��Ҳ����Ǯ48�ģ��ʼף��Ҷ���ԭ�����ж���Ǯ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com