
【题目】我市某中学对学校倡导的“压岁钱捐款活动”进行抽样调查,得到一组学生捐款的数据,
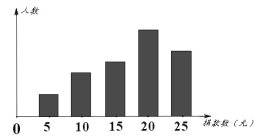
下图是根据这组数据绘制的统计图,图中从左到右长方形的高度之比为2:4:5:8:6.又知此次调查中捐款20元和25元的学生一共28人.
(1)他们一共调查了多少学生?
(2)写出这组数据的中位数、众数;
(3)若该校共有2000名学生,估计全校学生大约捐款多少元?
【答案】(1)50人(2)20,20(3)34800
【解析】(1)根据捐款20元和25与的学生一共是28人及这两组所占的总人数比例可求出总人数;
(2)众数即人数最多的捐款数,中位数要找到从小到大排列位于中间的数据;
(3)首先计算平均捐款数,再进一步估计总体平均捐款数,从而计算全校捐款数.
(1)(1)28÷![]() =50(名),
=50(名),
所以一共调查了50名学生;
(2)设捐款20元和25元的学生分别有8x人和6x人.
则有:8x+6x=28,
∴x=2
5个组的人数分别为4,8,10,16,12,
∴这组数据的中位数是20元,众数是20元;
(3)平均每个学生捐款的数量是:
![]() (5×4+10×8+15×10+20×16+25×12)=17.4(元),
(5×4+10×8+15×10+20×16+25×12)=17.4(元),
17.4×2000=34800(元),
所以全校学生大约捐款34800元.


科目:初中数学 来源: 题型:
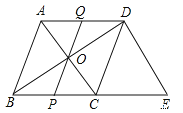
【题目】如图,在菱形ABCD中,对角线AC与BD相交于O点,AB=5,AC=6,过D点作DE//AC交BC的延长线于E点
(1)求△BDE的周长
(2)点P为线段BC上的点,连接PO并延长交AD于点Q,求证:BP=DQ
查看答案和解析>>
科目:初中数学 来源: 题型:
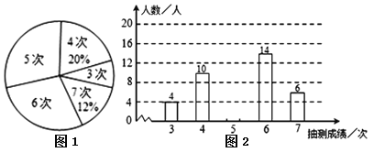
【题目】为了解某校八年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)本次抽测的男生有 人,抽测成绩的众数是 ;
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校400名八年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
A.
B.
C.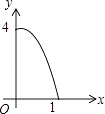
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D,E的运动时间为t秒,DF⊥BC于F
(1)求证:AE=DF;
(2)如图2,连接EF,![]()
①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由
②连接DE,当△DEF是直角三角形时,求t的值
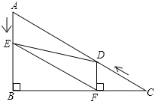
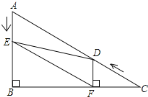

图1 图2 备用图 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、92、85.
①这组数据的众数是 , 中位数是;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
![]()
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com