
【题目】如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
A.
B.
C.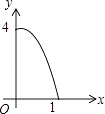
D.
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=4 ![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1. 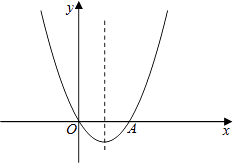
(1)常数m= , 点A的坐标为;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小为原来的一半,则线段AC的中点P变换后在第一象限对应点的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
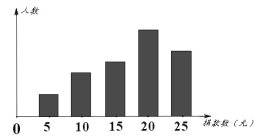
【题目】我市某中学对学校倡导的“压岁钱捐款活动”进行抽样调查,得到一组学生捐款的数据,
下图是根据这组数据绘制的统计图,图中从左到右长方形的高度之比为2:4:5:8:6.又知此次调查中捐款20元和25元的学生一共28人.
(1)他们一共调查了多少学生?
(2)写出这组数据的中位数、众数;
(3)若该校共有2000名学生,估计全校学生大约捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
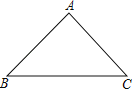
【题目】如图,已知△ABC
(1)用直尺和圆规作△ABC的边BC上的高AD,并在线段AD上找一点E,使E到AB的距离等于ED(不写作法,保留作图痕迹);
(2)若AB=AC=5,BC=6,求出ED的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
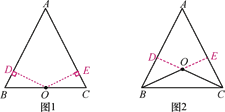
(1)如图1,若点O在BC上,求证:AB=AC.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)猜想,若点O在△ABC的外部,AB=AC成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com