
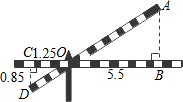
 如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米?
如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米? 分析 首先根据∠DCO=∠ABO=90°,∠AOB=∠COD,可得△CDO∽△BAO,进而可得$\frac{CD}{AB}$=$\frac{CO}{BO}$,再代入相应数据可得AB长.
解答 解:∵∠DCO=∠ABO=90°,∠AOB=∠COD,
∴△CDO∽△BAO,
∴$\frac{CD}{AB}$=$\frac{CO}{BO}$,
∴CO=1.25米,BO=5.5米,DC=0.85米,
∴$\frac{1.25}{5.5}$=$\frac{0.85}{AB}$,
解得:AB=3.74,
∴长臂端点升高3.74米.
点评 此题主要考查了相似三角形的应用,关键是掌握相似三角形对应边成比例.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
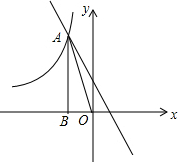 如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.
如图,Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△AOB=$\frac{3}{2}$,求这两个函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 44cm | B. | 40cm | C. | 36cm | D. | 24cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
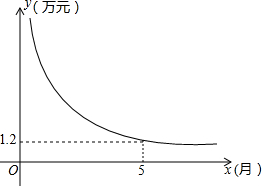 黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
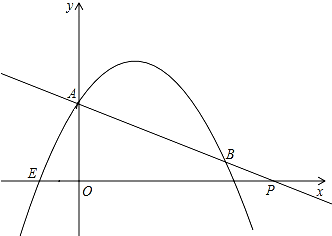 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c的图象过点E(-1,0)、点A(0,2)两点.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c的图象过点E(-1,0)、点A(0,2)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com