
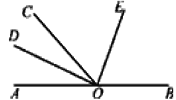
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
【答案】(1)9;(2)155°;(3)OE平分∠BOC,见解析
【解析】
(1)根据角的定义即可解决;
(2)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(3)根据∠COE=∠DOE-∠DOC和∠BOE=∠BOD-∠DOE分别求得∠COE与∠BOE的度数即可说明.
解:(1)图中小于平角的角∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB.共9个角.
(2)∵∠AOC=50°,OD平分∠AOC,
∴∠DOC= ![]() ∠AOC=25°,∠BOC=180°-∠AOC=130°,
∠AOC=25°,∠BOC=180°-∠AOC=130°,
∴∠BOD=∠DOC+∠BOC=155°.
(3)∵∠DOE=90°,∠DOC=25°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°.
又∵∠BOE=∠BOD-∠DOE=155°-90°=65°,
∴∠COE=∠BOE,
即OE平分∠BOC.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
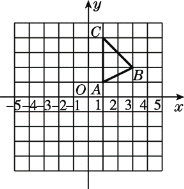
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
(1)将△ABC先向下平移4个单位,再向右平移1个单位,画出第二次平移后的△A1B1C1.若将△A1B1C1看成是△ABC经过一次平移得到的,则平移距离是________.
(2)以原点为对称中心,画出与△ABC成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
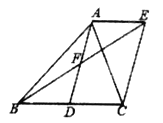
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:△AFE≌ODFB;
(2)求证:四边形ADCE是平行四边形;
(3)当AB、AC之间满足什么条件时,四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
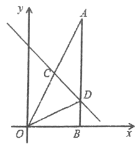
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
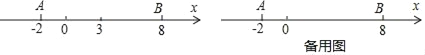
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
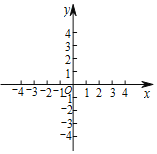
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com