
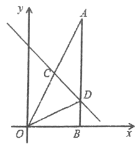
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
【答案】(1)y=2x; (2)![]() ;(3)点M的坐标为(
;(3)点M的坐标为(![]() ,0).
,0).
【解析】
(1)先求出点A的坐标,然后设直线AO的解析式为y=kx,用待定系数法求解即可;
(2)由面积法求出BD的长,从而求出点D的坐标,然后带入y=-x+b求解即可;
(3)先求出点C的坐标,作点C关于x轴的对称点E,此时M到A、C的距离之和最小,求出直线AE的解析式,即可求出点M的坐标.
(1)![]() OB=4,AB=8,∠ABO=90°,
OB=4,AB=8,∠ABO=90°,
∴A点坐标为(4,8),
设直线AO的解析式为y=kx,则4k=8 ,
解得k=2,即直线AO的解析式为y=2x;
(2)![]() OB=4,∠ABO=90°,
OB=4,∠ABO=90°,![]() =4,
=4,
∴DB=2,∴D点的坐标为(4,2),
把D(4,2)代入![]() 得:
得:![]() =6,
=6,
∴直线CD的解析式为![]() ;
;
(3)由直线![]() 与直线
与直线![]() 组成方程组为
组成方程组为![]() ,
,
解得:![]() ,
,
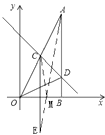
∴点C的坐标为(2,4)
如图,设点M使得MC+MA最小,作点C关于x轴的对称点E,可得点E的坐标为(2,-4),连结MC、ME、AE,可知MC=ME,所以M到A、C的距离之和MA+MC=MA+ME,又MA+ME大于等于AE,所以当MA+ME=AE时,M到A、C的距离之和最小,此时A、M、E成一条直线,M点是直线AE与在x轴的交点.
所以设直线AE的解析式为![]() ,把A(4,8)和E(2,-4)代入
,把A(4,8)和E(2,-4)代入![]() 得:
得:
![]() ,
,
解得:![]() ,
,
所以直线AE的解析式为![]() ,令
,令![]() 得
得![]() ,
,
所以点M的坐标为(![]() ,0).
,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
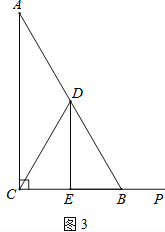
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
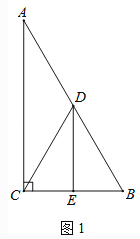
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
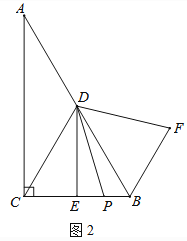
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
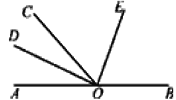
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试,面试中包括形体、口才、专业知识,他们的成绩(百分制)如下表:

(1)如果公司根据经营性质和岗位要求,以面试成绩中形体、口才、专业知识按照![]() 的比值确定成绩,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
的比值确定成绩,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
(2)如果公司根据经营性质和岗位要求,以面试成绩中形体占![]() ,口才占
,口才占![]() ,专业知识占
,专业知识占![]() 确定成绩,那么你认为该公司应该录取谁?
确定成绩,那么你认为该公司应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
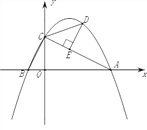
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
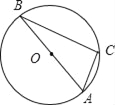
【题目】如图,⊙O是△ABC外接圆,直径AB=12,∠A=2∠B.
(1)∠A= °,∠B= °;
(2)求BC的长(结果用根号表示);
(3)连接OC并延长到点P,使CP=OC,连接PA,画出图形,求证:PA是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com