
【题目】如图, ![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 、
、![]() 作
作![]() ,
, ![]() ,连接
,连接![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,
, ![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)请问点![]() 在什么位置时,
在什么位置时, ![]() 的值最小,求出这个最小值;
的值最小,求出这个最小值;
(3)根据(2)中的规律和结论,构图求出代数式![]() 的最小值.
的最小值.
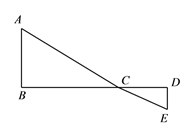
【答案】(1)用含x的代数式表示![]() 的长
的长![]()
(2)当A、C、E三点共线时![]() 取最小值,最小值为10;
取最小值,最小值为10;
(3)代数式最小值为![]()
【解析】试题分析:
试题分析:(1)由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;
(2)若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小;
(3)由(1)(2)的结果可作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,则AE的长即为代数式![]() +
+![]() 的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.
的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.
试题解析:(1)由勾股定理知
![]()
![]()
∴![]()
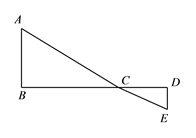
(2)当![]() 、
、![]() 、
、![]() 三点共线时
三点共线时![]() 取最小值,如下图
取最小值,如下图
∴在![]() 和
和![]() 中
中
![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴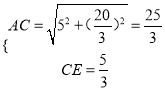
∴![]()
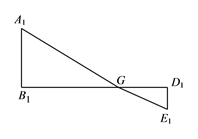
(3)根据(2)中规律可以构造出如图所示
由(2)中方法可得: ![]()
∴![]()
∴![]()
∴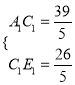
∴![]()
∴代数式最小值为![]()



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小丽想用一块面积为400平方厘米的正方形纸片,沿着边的方向裁出一块面积为300平方厘米的长方形纸片,使它的长宽之比为3:2.不知能否裁出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
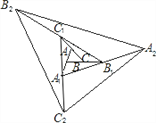
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0.
(1)当k为何值时,此方程有实数根;
(2)若此方程的两个实数根x1、x2满足|x1|+|x2|=3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x2﹣8x+15=0左边配成一个完全平方式后,所得的方程是( )
A.(x﹣6)2=1
B.(x﹣4)2=1
C.(x﹣4)2=31
D.(x﹣4)2=﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065m2.这个数用科学记数法表示为_____m2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com