
【题目】如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H. 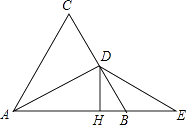
(1)求∠BAD和∠BDE的度数;
(2)求证:点H是AE的中点.
【答案】
(1)解:∵在等边△ABC,且D是AC的中点,
∴∠DAB= ![]() ∠BAC=
∠BAC= ![]() ×60°=30°,∠ABC=60°,
×60°=30°,∠ABC=60°,
∵BE=BD,
∴∠BDE=∠E,
∵∠ABC=∠BDE+∠E,
∴∠BDE=∠E=30°,
∴∠BAD=30°,∠BDE=30°
(2)证明:由(1)可知,∠DAB=∠E=30°
∴AD=ED,△ADE为等腰三角形,
又∵DH⊥AE,
∴H是AE的中点.
【解析】(1)根据等腰三角形的三线合一,可得∠DAB=30°,根据∠ABC=60°,BD=BE,推出∠E=30°.(2)要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形的高和中线向重合即可得证.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】今年是襄阳“创建文明城市”工作的第二年,为了更好地做好“创建文明城市”工作,市教育局相关部门对某中学学生“创文”的知晓率,采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”, “比校了解”, “基本了解”,和“不了解”四个等级.小辉根据调查结果绘制了如图所示的统计图,请根据提供的信息回答问题:
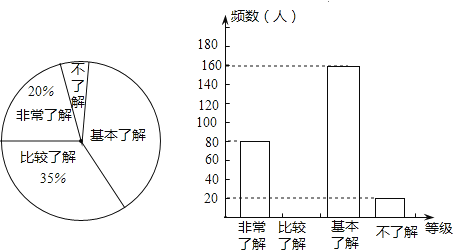
(1)本次调查中,样本容量是_________;
(2)扇形统计图中“基本了解”部分所对应的圆心角的度数是_______;在该校2000名学生中随机提问一名学生,对“创文”不了解的概率估计值为________
(3)请补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
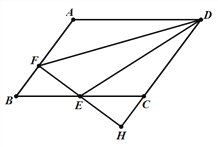
【题目】如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一粒大米的质量约为0.0000021千克,这个数用科学记数法表示为( )
A.0.21×10﹣5
B.2.1×10﹣5
C.2.1×10﹣6
D.21×10﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com