
ΓΨΧβΡΩΓΩΈΣ¬ζΉψ –≥Γ–η«σΘ§–¬…ζΜν≥§ –‘ΎΕΥΈγΫΎ«ΑœΠΙΚΫχΦέΗώΈΣ![]() ‘Σ/ΗωΒΡτ’Ή”Θ§ΗυΨί –≥Γ‘Λ≤βΘ§ΗΟΤΖ≈Ττ’Ή”ΟΩΗω έΦέ
‘Σ/ΗωΒΡτ’Ή”Θ§ΗυΨί –≥Γ‘Λ≤βΘ§ΗΟΤΖ≈Ττ’Ή”ΟΩΗω έΦέ![]() ‘Σ ±Θ§ΟΩΧλΡή≥ω έ
‘Σ ±Θ§ΟΩΧλΡή≥ω έ![]() ΗωΘ§≤Δ«“ έΦέΟΩ…œ’«
ΗωΘ§≤Δ«“ έΦέΟΩ…œ’«![]() ‘ΣΘ§Τδœζ έΝΩΫΪΦθ…Ό
‘ΣΘ§Τδœζ έΝΩΫΪΦθ…Ό![]() ΗωΘ§ΈΣΝΥΈ§ΜΛœϊΖ―’Ώάϊ“φΘ§ΈοΦέ≤ΩΟ≈ΙφΕ®Θ§ΗΟΤΖ≈Ττ’Ή”ΒΡ έΦέ≤ΜΡή≥§ΙΐΫχΦέΒΡ
ΗωΘ§ΈΣΝΥΈ§ΜΛœϊΖ―’Ώάϊ“φΘ§ΈοΦέ≤ΩΟ≈ΙφΕ®Θ§ΗΟΤΖ≈Ττ’Ή”ΒΡ έΦέ≤ΜΡή≥§ΙΐΫχΦέΒΡ![]() Θ°
Θ°
Θ®1Θ©«κΡψάϊ”ΟΥυ―ß÷Σ ΕΑο÷ζ≥§ –ΗχΗΟΤΖ≈Ττ’Ή”Ε®ΦέΘ§ Ι≥§ –ΟΩΧλΒΡœζ έάϊ»σΈΣ![]() ‘ΣΘ°
‘ΣΘ°
Θ®2Θ©Ε®ΦέΈΣΕύ…Ό ±ΟΩΧλΒΡάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©Ε®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ![]() ‘ΣΘΜΘ®2Θ©Β±Ε®ΦέΈΣ
‘ΣΘΜΘ®2Θ©Β±Ε®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΉν¥σΘ§Ήν¥σΒΡάϊ»σ «
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΉν¥σΘ§Ήν¥σΒΡάϊ»σ «![]() ‘ΣΘ°
‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ![]() ‘ΣΘ§ΗυΨίΓΑΉήάϊ»σ=ΒΞΗωάϊ»σΓΝ ΐΝΩΓ±Ν–≥ωΖΫ≥ΧΦ¥Ω…«σ≥ωΫα¬έΘΜ
‘ΣΘ§ΗυΨίΓΑΉήάϊ»σ=ΒΞΗωάϊ»σΓΝ ΐΝΩΓ±Ν–≥ωΖΫ≥ΧΦ¥Ω…«σ≥ωΫα¬έΘΜ
Θ®2Θ©…ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ![]() ‘ΣΘ§ΗυΨίΓΑΉήάϊ»σ=ΒΞΗωάϊ»σΓΝ ΐΝΩΓ±Φ¥Ω…±μ Ψ≥ωΉήάϊ»σΘ§»ΜΚσάϊ”Ο≈δΖΫΖ®ΚΆΤΫΖΫΒΡΖ«ΗΚ–‘Φ¥Ω…«σ≥ωΫα¬έΘ°
‘ΣΘ§ΗυΨίΓΑΉήάϊ»σ=ΒΞΗωάϊ»σΓΝ ΐΝΩΓ±Φ¥Ω…±μ Ψ≥ωΉήάϊ»σΘ§»ΜΚσάϊ”Ο≈δΖΫΖ®ΚΆΤΫΖΫΒΡΖ«ΗΚ–‘Φ¥Ω…«σ≥ωΫα¬έΘ°
ΫβΘΚ![]() …ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ
…ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ![]() ‘ΣΘ§
‘ΣΘ§
ΗυΨίΧβ“βΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟ![]()
“ρ έΦέ≤ΜΡή≥§ΙΐΫχΦέΒΡ![]() Θ§
Θ§
Ι ![]() Θ§Φ¥
Θ§Φ¥![]()
![]() Θ§Φ¥Ε®ΦέΈΣ
Θ§Φ¥Ε®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΈΣ![]() ‘ΣΘ°
‘ΣΘ°
![]() …ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ
…ηΟΩΗωτ’Ή”ΒΡΕ®ΦέΈΣ![]() ‘ΣΘ§‘ρΟΩΧλΒΡάϊ»σΈΣΘΚ
‘ΣΘ§‘ρΟΩΧλΒΡάϊ»σΈΣΘΚ
![]()
![]()
![]()
![]()
![]()
![]() Β±Ε®ΦέΈΣ
Β±Ε®ΦέΈΣ![]() ‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΉν¥σΘ§Ήν¥σΒΡάϊ»σ «
‘Σ ±Θ§ΟΩΧλΒΡάϊ»σΉν¥σΘ§Ήν¥σΒΡάϊ»σ «![]() ‘ΣΘ°
‘ΣΘ°


 Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ―ßΩΈ…œΘ§άœ ΠΧα≥ω“ΜΗωΈ ΧβΘΚ»γΆΦΔΌΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() «
«![]() ÷α’ΐΑκ÷α…œ“ΜΕ·ΒψΘ§“‘
÷α’ΐΑκ÷α…œ“ΜΕ·ΒψΘ§“‘![]() ΈΣ±ΏΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΈΣ±ΏΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ![]() Θ§ Ι
Θ§ Ι![]() Θ§Βψ
Θ§Βψ![]() ‘ΎΒΎ“ΜœσœόΘ§…ηΒψ
‘ΎΒΎ“ΜœσœόΘ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§…ηΓ≠Γ≠ΈΣ
Θ§…ηΓ≠Γ≠ΈΣ![]() Θ§
Θ§![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΆΦœσ»γΆΦΔΎΥυ ΨΘ°Χβ÷–”ΟΓΑΓ≠Γ≠Γ±±μ ΨΒΡ»± ßΒΡΧθΦΰ”Π≤ΙΈΣΘ® Θ©
÷°ΦδΒΡΚ· ΐΆΦœσ»γΆΦΔΎΥυ ΨΘ°Χβ÷–”ΟΓΑΓ≠Γ≠Γ±±μ ΨΒΡ»± ßΒΡΧθΦΰ”Π≤ΙΈΣΘ® Θ©


A.Βψ![]() ΒΡΚαΉχ±ξB.Βψ
ΒΡΚαΉχ±ξB.Βψ![]() ΒΡΉίΉχ±ξC.
ΒΡΉίΉχ±ξC.![]() ΒΡ÷ή≥ΛD.
ΒΡ÷ή≥ΛD.![]() ΒΡΟφΜΐ
ΒΡΟφΜΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ¬δ ΒΙζΈώ‘ΚΒΡ÷Η ΨΨΪ…ώΘ§Ρ≥ΒΊΖΫ’ΰΗ°≥ωΧ®ΝΥ“ΜœΒΝ–ΓΑ»ΐ≈©Γ±”≈Μί’ΰ≤ΏΘ§ Ι≈©Οώ ’»κ¥σΖυΕ»‘ωΦ”Θ°Ρ≥≈©Μß…ζ≤ζΨ≠œζ“Μ÷÷≈©≤ζΤΖΘ§“―÷Σ’β÷÷≤ζΤΖΒΡ≥…±ΨΦέΈΣΟΩ«ßΩΥ20‘ΣΘ§ –≥ΓΒς≤ιΖΔœ÷Θ§ΗΟ≤ζΤΖΟΩΧλΒΡœζ έΝΩy(«ßΩΥ)”κœζ έΦέx(‘Σ/«ßΩΥ)”–»γœ¬ΙΊœΒΘΚyΘΫΘ≠2xΘΪ80.…η’β÷÷≤ζΤΖΟΩΧλΒΡœζ έάϊ»σΈΣw‘ΣΘ°
Θ®1Θ©«σw”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©ΗΟ≤ζΤΖœζ έΦέΕ®ΈΣΟΩ«ßΩΥΕύ…Ό‘Σ ±Θ§ΟΩΧλΒΡœζ έάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…Ό‘ΣΘΩ
Θ®3Θ©»γΙϊΈοΦέ≤ΩΟ≈ΙφΕ®’β÷÷≤ζΤΖΒΡœζ έΦέ≤ΜΗΏ”ΎΟΩ«ßΩΥ28‘ΣΘ§ΗΟ≈©Μßœκ“ΣΟΩΧλΜώΒΟ150‘ΣΒΡœζ έάϊ»σΘ§œζ έΦέ”ΠΕ®ΈΣΟΩ«ßΩΥΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΨ≠Ιΐ‘≠ΒψΒΡ≈ΉΈοœΏ ![]() ”κ
”κ ![]() ÷αΒΡΝμ“ΜΗωΫΜΒψΈΣ
÷αΒΡΝμ“ΜΗωΫΜΒψΈΣ ![]() Θ§œ÷ΫΪ≈ΉΈοœΏœρ”“ΤΫ“Τ
Θ§œ÷ΫΪ≈ΉΈοœΏœρ”“ΤΫ“Τ ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΥυΒΟ≈ΉΈοœΏ”κ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΥυΒΟ≈ΉΈοœΏ”κ ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ ![]() Θ§”κ‘≠≈ΉΈοœΏΫΜ”ΎΒψ
Θ§”κ‘≠≈ΉΈοœΏΫΜ”ΎΒψ ![]() Θ§…η
Θ§…η ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ ![]() Θ§‘ρ”Ο
Θ§‘ρ”Ο ![]() ±μ Ψ
±μ Ψ ![]() =
=
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2020ΡξΡβΦΧ–χΨΌΑλάωΥ° –÷–―ß…ζΚΚΉ÷Χΐ–¥ΓΔ Ϊ¥ Υ––¥¥σ»ϋΘ°Ψ≠Ιΐ≥θ»ϋΓΔΗ¥»ϋΘ§―Γ≥ωΝΥΝΫΗω¥ζ±μΕ”≤ΈΦ” –ΡΎ7‘¬ΖίΒΡΨω»ϋΘ°ΝΫΗωΕ”Ης―Γ≥ωΒΡ![]() Οϊ―Γ ÷ΒΡΗ¥»ϋ≥…Φ®»γΆΦΥυ ΨΘ°
Οϊ―Γ ÷ΒΡΗ¥»ϋ≥…Φ®»γΆΦΥυ ΨΘ°
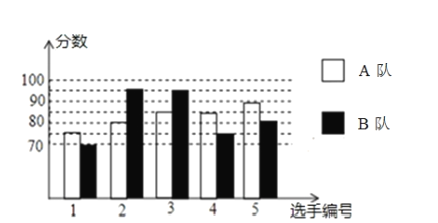
Θ®1Θ©ΗυΨίΆΦ Ψ≤Ι»Ϊœ¬±μΘΜ
ΤΫΨυ ΐ(Ζ÷) | ÷–ΈΜ ΐ(Ζ÷) | ÷Ύ ΐ(Ζ÷) | |
|
|
| |
|
|
Θ®2Θ©ΫαΚœΝΫΕ”≥…Φ®ΒΡΤΫΨυ ΐΚΆ÷–ΈΜ ΐΘ§Ζ÷ΈωΡΡΗωΕ”ΒΡΗ¥»ϋ≥…Φ®ΫœΚΟΘΜ
Θ®3Θ©ΦΤΥψΝΫΕ”≥…Φ®ΒΡΖΫ≤νΘ§≤Δ≈–ΕœΡΡ“ΜΗω¥ζ±μΕ”―Γ ÷≥…Φ®ΫœΈΣΈ»Ε®Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Φ“ΒγΦ·Ά≈ΙΪΥΨ―–÷Τ…ζ≤ζΒΡ–¬Φ“ΒγΘ§«ΑΤΎΆΕΉ ![]() Άρ‘ΣΘ§ΟΩ…ζ≤ζ“ΜΧ®’β÷÷–¬Φ“ΒγΘ§ΚσΤΎΜΙ–ηΤδΥϊΆΕΉ
Άρ‘ΣΘ§ΟΩ…ζ≤ζ“ΜΧ®’β÷÷–¬Φ“ΒγΘ§ΚσΤΎΜΙ–ηΤδΥϊΆΕΉ ![]() Άρ‘ΣΘ§“―÷ΣΟΩΧ®–¬Φ“Βγ έΦέΈΣ
Άρ‘ΣΘ§“―÷ΣΟΩΧ®–¬Φ“Βγ έΦέΈΣ ![]() Άρ‘ΣΘ§…ηΉήΆΕΉ ΈΣ
Άρ‘ΣΘ§…ηΉήΆΕΉ ΈΣ![]() Άρ‘ΣΘ®ΉήΆΕΉ
Άρ‘ΣΘ®ΉήΆΕΉ ![]() «ΑΤΎΆΕΉ
«ΑΤΎΆΕΉ ![]() ΚσΤΎΆΕΉ Θ©Θ§Ήήάϊ»σΈΣ
ΚσΤΎΆΕΉ Θ©Θ§Ήήάϊ»σΈΣ![]() Άρ‘ΣΘ®Ήήάϊ»σ
Άρ‘ΣΘ®Ήήάϊ»σ![]() Ήή έΦέ
Ήή έΦέ![]() ΉήΆΕΉ Θ©Θ§–¬Φ“ΒγΉή≤ζΝΩΈΣ
ΉήΆΕΉ Θ©Θ§–¬Φ“ΒγΉή≤ζΝΩΈΣ![]() Χ®Θ§Θ®ΦΌ…ηΩ…Α¥≤ζΝΩ»Ϊ≤Ω¬τ≥ωΘ©
Χ®Θ§Θ®ΦΌ…ηΩ…Α¥≤ζΝΩ»Ϊ≤Ω¬τ≥ωΘ©
Θ®1Θ© ‘”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ
ΒΡ¥ζ ΐ Ϋ±μ Ψ![]() ΚΆ
ΚΆ![]() ΘΜ
ΘΜ
Θ®2Θ©Έ –¬Φ“ΒγΉή≤ζΝΩ≥§ΙΐΕύ…ΌΧ® ±Θ§ΗΟΙΪΥΨΩΣ Φ”·άϊ?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAD «Β»―ϋΓςABCΒΉ±ΏBC…œΒΡΗΏΘ§sinB= ![]() Θ§ΒψE‘ΎAC…œΘ§«“AEΘΚEC=2ΘΚ3Θ§‘ρtanΓœADE=Θ® Θ©
Θ§ΒψE‘ΎAC…œΘ§«“AEΘΚEC=2ΘΚ3Θ§‘ρtanΓœADE=Θ® Θ© 
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊ»ΐΫ«–Έ”–“Μ±Ώ…œΒΡ÷–œΏ≥Λ«ΓΚΟΒ»”Ύ’β±ΏΒΡ≥ΛΘ§Ρ«Ο¥≥Τ’βΗω»ΐΫ«–ΈΈΣΓΑΚΟΆφ»ΐΫ«–ΈΓ±Θ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§»τRtΓςABC «ΓΑΚΟΆφ»ΐΫ«–ΈΓ±Θ§‘ρtanA= Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§»ΐΫ«–ΈABO÷–Θ§AΘ®©¹2Θ§©¹3Θ©ΓΔBΘ®2Θ§©¹1Θ©Θ§»ΐΫ«–ΈAΓδBΓδOΓδ «»ΐΫ«–ΈABOΤΫ“Τ÷°ΚσΒΟΒΫΒΡΆΦ–ΈΘ§≤Δ«“OΒΡΕ‘”ΠΒψOΓδΒΡΉχ±ξΈΣΘ®4Θ§3Θ©.
Θ®1Θ©«σ»ΐΫ«–ΈABOΒΡΟφΜΐ;
Θ®2Θ©Ής≥ω»ΐΫ«–ΈABOΤΫ“Τ÷°ΚσΒΡΆΦ–Έ»ΐΫ«–ΈAΓδBΓδOΓδ,≤Δ–¥≥ωAΓδΓΔBΓδΝΫΒψΒΡΉχ±ξΖ÷±πΈΣAΓδΓΓΓΓΓΓΓΔBΓδΓΓΓΓΓΓΘΜ
Θ®3Θ©PΘ®xΘ§yΘ©ΈΣ»ΐΫ«–ΈABO÷–»Έ“β“ΜΒψΘ§‘ρΤΫ“ΤΚσΕ‘”ΠΒψPΓδΒΡΉχ±ξΈΣ__________.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com