
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
科目:初中数学 来源: 题型:
【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠15% |
乙商场 | 每台优惠10% |
(1)设公司购买![]() 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为![]() 元/个的粽子,根据市场预测,该品牌粽子每个售价
元/个的粽子,根据市场预测,该品牌粽子每个售价![]() 元时,每天能出售
元时,每天能出售![]() 个,并且售价每上涨
个,并且售价每上涨![]() 元,其销售量将减少
元,其销售量将减少![]() 个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的
个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的![]() .
.
(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为![]() 元.
元.
(2)定价为多少时每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界读书日,某书店举办“书香”图书展,已知《汉语成语大词典》和《中华上 下五千年》两本书的标价总和为![]() 元,《汉语成语大词典》按标价的
元,《汉语成语大词典》按标价的![]() 折出售,《中华 上下五千年》按标价的
折出售,《中华 上下五千年》按标价的![]() 折出售,小明花
折出售,小明花![]() 元买了这两本书,求这两本书的标价各多少元?
元买了这两本书,求这两本书的标价各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到![]() .
.

(1)画出平移后的![]() ;
;
(2)写出![]() 三个顶点的坐标;
三个顶点的坐标;
(3)已知点P在x轴上,以![]() 、
、![]() 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD的平分线AE与∠BCD的平分线CE交于点E,若∠B=38°,∠D=20°,则∠AEC的度数为
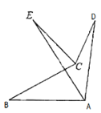
A. 9°B. 18°C. 22°D. 29°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线 ![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥ ![]() 于点D.
于点D.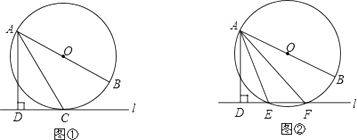
(1)如图①,当直线 ![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线 ![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)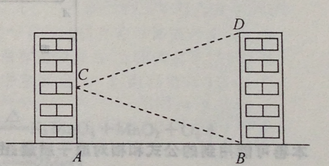
(1)求∠BCD的度数.
(2)求教学楼的高BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com