
【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠15% |
乙商场 | 每台优惠10% |
(1)设公司购买![]() 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,两商场收费相同,当
时,两商场收费相同,当![]() 时,到甲商场购买更优惠,当
时,到甲商场购买更优惠,当![]() 时,到乙商场购买更优惠;(3)当
时,到乙商场购买更优惠;(3)当![]() 取最大值4时,
取最大值4时,![]() 取到最小值,为180元.
取到最小值,为180元.
【解析】
(1)分别根据甲商场和乙商场的优惠条件列式整理即可;
(2)分别根据题意列出方程或不等式,求解即可;
(3)根据题意列出![]() 关于m的一次函数关系式,然后根据一次函数的性质求解即可.
关于m的一次函数关系式,然后根据一次函数的性质求解即可.
解:(1)由题意得:![]() ,
,
![]() ;
;
(2)若收费相同,则![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
若是到甲商场购买更优惠,则![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
若是到甲乙商场购买更优惠,则![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
答:当![]() 时,两商场收费相同,当
时,两商场收费相同,当![]() 时,到甲商场购买更优惠,当
时,到甲商场购买更优惠,当![]() 时,到乙商场购买更优惠;
时,到乙商场购买更优惠;
(3)依题意,有:![]() ,
,
由于甲商场库存只有4台,所以:![]() ,
,
∵![]() ,
,
∴![]() 随着
随着![]() 的增大而减小,
的增大而减小,
∴当![]() 取最大值4时,
取最大值4时,![]() 取到最小值,为180元.
取到最小值,为180元.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE, 则线段DE与线段AC有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师提出一个问题:如图①,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一动点,以
轴正半轴上一动点,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,使
,使![]() ,点
,点![]() 在第一象限,设点
在第一象限,设点![]() 的横坐标为
的横坐标为![]() ,设……为
,设……为![]() ,
,![]() 与
与![]() 之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )
之间的函数图象如图②所示.题中用“……”表示的缺失的条件应补为( )


A.点![]() 的横坐标B.点
的横坐标B.点![]() 的纵坐标C.
的纵坐标C.![]() 的周长D.
的周长D.![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)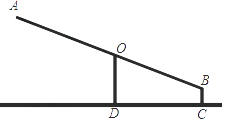
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m,一面旧墙壁AB的长为x m,修建健身房墙壁的总投入为y元.
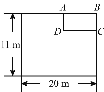
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12,当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知经过原点的抛物线 ![]() 与
与 ![]() 轴的另一个交点为
轴的另一个交点为 ![]() ,现将抛物线向右平移
,现将抛物线向右平移 ![]() 个单位长度,所得抛物线与
个单位长度,所得抛物线与 ![]() 轴交于
轴交于 ![]() ,与原抛物线交于点
,与原抛物线交于点 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,则用
,则用 ![]() 表示
表示 ![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com