Question

【题目】如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y= x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是 ．

Answer 1

【答案】﹣2＜k＜
【解析】解：由图可知，∠AOB=45°， ∴直线OA的解析式为y=x，
联立 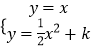消掉y得，
x2﹣2x+2k=0，
△=b2﹣4ac=（﹣2）2﹣4×1×2k=0，
即k= 时，抛物线与OA有一个交点，
此交点的横坐标为1，
∵点B的坐标为（2，0），
∴OA=2，
∴点A的坐标为（ ， ），
∴交点在线段AO上；
当抛物线经过点B（2，0）时， ×4+k=0，
解得k=﹣2，
∴要使抛物线y= x2+k与扇形OAB的边界总有两个公共点，实数k的取值范围是﹣2＜k＜ ．
故答案为：﹣2＜k＜ ．
根据∠AOB=45°求出直线OA的解析式，然后与抛物线解析式联立求出有一个公共点时的k值，即为一个交点时的最大值，再求出抛物线经过点B时的k的值，即为一个交点时的最小值，然后写出k的取值范围即可．