【题目】如图所示，在□ABCD中，E，F分别在BC，AD上，若想使四边形AFCE为平行四边形，须添加一个条件，这个条件可以是（ ）
①AF=CF；②AE=CF；③∠BAE=∠FCD；④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
名校课堂系列答案科目：初中数学 来源： 题型：
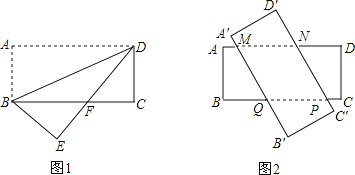
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′，其中AB=3，BC=8．
（1）若将其中一张矩形纸片ABCD沿着BD折叠，点A落在点E处（如图1），设DE与BC相交于点F，求BF的长；
（2）若将这两张矩形纸片交叉叠放（如图2），判断四边形MNPQ的形状，并证明．四边形MNPQ的最大面积是_________.（直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（ 
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
小明在一本课外读物上看到一道有意思的数学题：例1、解不等式：
，根据绝对值的几何意义，到原点距离小于1的点在数轴上集中在－1和+1之间，如图:
所以，该不等式的解集为－1<x<1．
因此，不等式
的解集为x<－1或x>1．
根据以上方法小明继续探究：例2：求不等式：
的解集，即求到原点的距离大于2小于5的点的集合就集中在这样的区域内，如图：
所以，不等式的解集为－5<x<－2或2<x<5．
仿照小明的做法解决下面问题：
（1）不等式
的解集为____________．
（2）不等式
的解集是____________．
（3）求不等式
的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
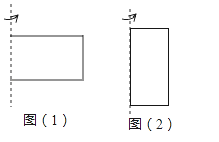
【题目】如图，长方形的长和宽分别是7cm和3cm，分别绕着它的长和宽所在的直线旋转一周，回答下列问题：
（1）如图（1），绕着它的宽所在的直线旋转一周，所得到的是什么样的几何体？得到的几何体的体积是多少？（π取3.14）
（2）如图（2），绕着它的长所在的直线旋转一周，所得到的是什么样的几何体？得到的几何体的体积是多少？（π取3.14）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y= 
x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并说明你猜想的正确性．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】顺次连接四边形各边中点，所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
