
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
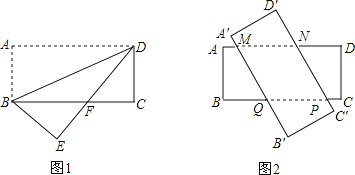
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
【答案】①BF=![]() ②
②![]()
【解析】试题分析:
(1)由折叠的性质结合AD∥BC易得∠FBD=∠ADB=∠FDB,由此可得BF=DF,设BF=x,结合DE=AD=BC=8,可得EF=8-x,结合BE=AB=3,在Rt△BEF中由勾股定理建立方程即可求得BF的值;
(2)①如图3,过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,则易证△QEP≌△NFP,从而可得PQ=PN,由已知条件易证四边形MNPQ是平行四边形,两者结合即可得到四边形MNPQ是菱形;
②如图4,由题意可知,菱形MNPQ边上的高是3,故当边长越长时,面积越大,由题意可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,在Rt△ABQ中,由勾股定理建立方程解出MQ的长,即可求得最大面积了.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=8,
∴∠ADB=∠DBC,
由折叠的性质可知,∠ADB=∠FDB,BE=AB=3,DE=AD=8,
∴∠DBC=∠FDB,
∴BF=DF,
设BF=x,则DF=x,
∴EF=8-x,
∵在Rt△BEF中,BF2=BE2+EF2,
∴![]() ,解得:
,解得: ![]() ;
;
(2)①如图2,四边形MNPQ是菱形,理由如下:
过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,
∴∠PEQ=∠PFN=90°,
∵两张纸条等宽,
∴NF=QE,
∵∠NPF=∠QPE,
∴△QEP≌△NFP,
∴PQ=PN,
∵由题意可得:MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形,
∴四边形MNPQ是菱形;

②如图4,由题意和①可知,菱形MNPQ边上的高是3,故当菱形MNPQ的边长越长时,其面积越大,由图4可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,
设AQ=QP=a,则BQ=BC-QC=8-a,
∵在Rt△ABQ中,AQ2=AB2+BQ2,
∴![]() ,解得:
,解得: ![]() ,
,
∴菱形MNPQ的最大面积为: ![]() .
.



 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y= ![]() x2+1(如图所示).
x2+1(如图所示).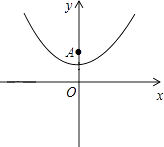
(1)填空:抛物线的顶点坐标是( , ),对称轴是;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
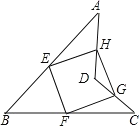
【题目】如图,E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状,并说明你的理由;
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形?证明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: 作法:如图,
⑴在射线OA上任取一点C,过点C作CD∥OB;
⑵以点C为圆心,CO的长为半径作弧,交CD于点E;
⑶作射线OE.
所以射线OE就是∠AOB的角平分线.请回答:小米的作图依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标xOy中,直线y=kx+1(k≠0)与双曲线y= ![]() (m≠0)的一个交点为A(﹣2,3),与x轴交于点B.
(m≠0)的一个交点为A(﹣2,3),与x轴交于点B. 
(1)求m的值和点B的坐标;
(2)点P在y轴上,点P到直线y=kx+1(k≠0)的距离为 ![]() ,直接写出点P的坐标.
,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)求该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
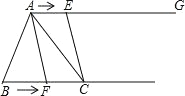
【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以![]() cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com