
【题目】小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: 作法:如图,
⑴在射线OA上任取一点C,过点C作CD∥OB;
⑵以点C为圆心,CO的长为半径作弧,交CD于点E;
⑶作射线OE.
所以射线OE就是∠AOB的角平分线.请回答:小米的作图依据是 .
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与C重合,折痕EF交AD于E,交BC于F,交AC于O,连结AF、CE. 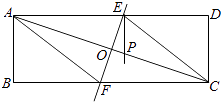
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:AE2=AOAP;
(3)若AE=8,△ABF的面积为9,求AB+BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
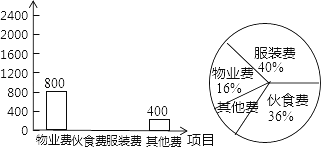
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
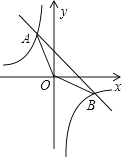
(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
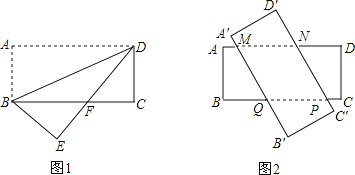
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:![]() ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
![]()
所以,该不等式的解集为-1<x<1.
因此,不等式![]() 的解集为x<-1或x>1.
的解集为x<-1或x>1.
根据以上方法小明继续探究:例2:求不等式:![]() 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
![]()
所以,不等式![]() 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)不等式![]() 的解集为____________.
的解集为____________.
(2)不等式![]() 的解集是____________.
的解集是____________.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com