Question

【题目】顺次连接四边形各边中点，所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。

Answer 1

【答案】平行四边形 互相垂直 相等 互相垂直且相等

【解析】试题解析：顺次连接四边形各边中点，所得的图形是平行四边形；

(如图)

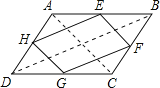
根据中位线定理可得： 且GF∥BD， 且EH∥BD，

∴EH=FG，EH∥FG，

∴四边形EFGH是平行四边形；

顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形；

如图：

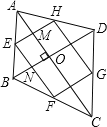
∵E、F.G、H分别为各边中点，

∴EF∥GH∥DB， ，

EH∥FG∥BD，

∵DB⊥AC，

∴EF⊥EH，

∴四边形EFGH是矩形；

顺次连接对角线相等的四边形的各边中点所得的四边形是菱形；

如图，

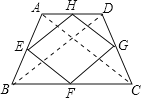
∵AC=BD，E. F.G、H分别是线段AB、BC、CD、AD的中点

∴EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线

根据三角形的中位线的性质，

∴

∵AC=BD，

∴EH=FG=FG=EF，

∴四边形EFGH是菱形；

根据正方形的判别方法知，对角线互相平分，互相垂直且相等的四边形是正方形.

故答案为：平行四边形、互相垂直、相等、互相垂直且相等.