
【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,

(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
【答案】见解析
【解析】试题分析:(1)先证得△ADB≌△CDB求得∠BCD=∠BAD,从而得到∠ADF=∠BAD,所以AB∥FD,因为BD⊥AC,AF⊥AC,所以AF∥BD,即可证得.
(2)先证得平行四边形是菱形,然后根据勾股定理即可求得.
试题解析:(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
 ,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5-x,
∴AB2-BE2=AD2-DE2,
即52-x2=62-(5-x)2
解得:x=![]() ,
,
∴![]() ,
,
∴AC=2AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:![]() ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
![]()
所以,该不等式的解集为-1<x<1.
因此,不等式![]() 的解集为x<-1或x>1.
的解集为x<-1或x>1.
根据以上方法小明继续探究:例2:求不等式:![]() 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
![]()
所以,不等式![]() 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)不等式![]() 的解集为____________.
的解集为____________.
(2)不等式![]() 的解集是____________.
的解集是____________.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= ![]() x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器经营业主两次购进一批同种型号的挂式空调和电风扇,第一次购进8台空调和20台电风扇;第二次购进10台空调和30台电风扇.![]() 若第一次用资金17400元,第二次用资金22500元,求挂式空调和电风扇每台的采购价各是多少元?
若第一次用资金17400元,第二次用资金22500元,求挂式空调和电风扇每台的采购价各是多少元?![]() 在
在![]() 的条件下,若该业主计划再购进这两种电器70台,而可用于购买这两种电器的资金不超过30000元,问该经营业主最多可再购进空调多少台?
的条件下,若该业主计划再购进这两种电器70台,而可用于购买这两种电器的资金不超过30000元,问该经营业主最多可再购进空调多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )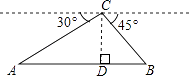
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() +1)米
+1)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级四个班的学生在植树节这天共义务植树(6a-3b)棵,一班植树a棵,二班植树的棵数比一班的两倍少b棵,三班植树的棵数比二班的一半多1棵.
(1)求三班的植树棵数(用含a,b的式子表示);
(2)求四班的植树棵数(用含a,b的式子表示);
(3)若四个班共植树54棵,求二班比三班多植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com