
 如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.分析 (1)连结OC,如图,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于CD⊥AD,所以OC⊥CD,则根据切线的判定定理得到DC为⊙O切线;
(2)①连结BC,如图,在Rt△ACD中利用勾股定理计算出AD=2,再Rt△ACD∽Rt△ABC,利用相似比计算出AB=$\frac{5}{2}$,从而得到⊙O半径长为$\frac{5}{4}$;
②证明△POC∽△PAD,然后利用相似比可计算出BP的长.
解答 (1)证明:连结OC,如图,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥CD,
∴DC为⊙O切线;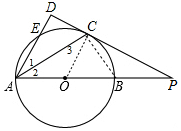
(2)解:①连结BC,如图,
在Rt△ACD中,∵CD=1,AC=$\sqrt{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=2,
∵AB为直径,
∴∠ACB=90°,
∵∠1=∠2,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,即$\sqrt{5}$:AB=2:$\sqrt{5}$,
∴AB=$\frac{5}{2}$,
∴⊙O半径长为$\frac{5}{4}$;
②∵OC∥AD,
∴△POC∽△PAD,
∴$\frac{PO}{PA}$=$\frac{OC}{AD}$,即$\frac{PB}{PB+\frac{5}{2}}$=$\frac{\frac{5}{4}}{2}$,
∴BP=$\frac{5}{6}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
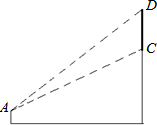 合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)
合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4,精确到十分位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将如图所示的A、B两组扑克牌分别洗匀后,背面朝上放置在桌面上.若分别从A、B两组牌中各随机抽取1张牌,求抽到2张牌的牌面数字之和是偶数的概率(用树状图或列表法求解).
将如图所示的A、B两组扑克牌分别洗匀后,背面朝上放置在桌面上.若分别从A、B两组牌中各随机抽取1张牌,求抽到2张牌的牌面数字之和是偶数的概率(用树状图或列表法求解).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com