
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 . 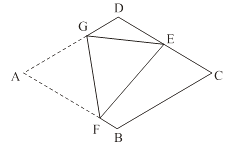
【答案】![]()
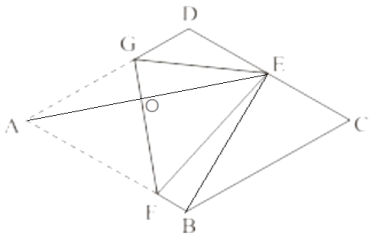
【解析】解:连接BE、AE交FG于点O,
∵菱形ABCD中,AB=2,∠A=60°,E为CD中点,
∴BE⊥CD,CE=1,BC=2,∠C=60°,∠ABC=120°,
∴BE=![]() ,∠CBE=30°,
,∠CBE=30°,
∴∠FBE=90°,
∴AE=![]() =
=![]() =
=![]() .
.
∵△AGF翻折至△EGF,
∴△AGF≌△EGF,
∴AF=EF,∠AFG=∠EFG,
在Rt△EBF中,设BF=x,则AF=EF=2-x,
∴(2-x)2=x2+(![]() )2
)2
∴x=![]() ,EF=
,EF=![]() ,
,
又∵AG=EG,AF=EF,
∴GF垂直平分AE,
∴EO=![]() .
.
∴FO=![]() =
=![]() =
=![]()
在Rt△EOF中.
∴cos∠EFG=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
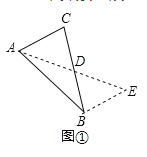

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数 y=2x 与 y=ax+5 的图象相交于点 A(m,4).
(1)求 A 点坐标及一次函数 y=ax+5 的解析式;
(2)设直线 y=ax+5 与 x 轴交于点 B,求△AOB 的面积;
(3)求不等式 2x<ax+5 的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)条件下,连结BD,当∠A=32°时,求∠CBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
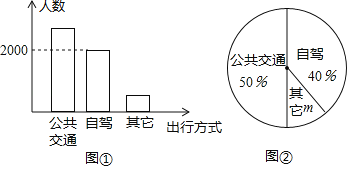
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
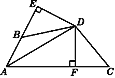
【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;

(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;

(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
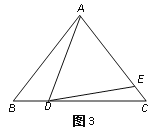
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布的扇形统计图,其中八年级人数为408人,下表是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人阅读课外书________本.
图书种类 | 频数 | 频率 |
科普知识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛记 | A | 0.25 |
其他 | 144 | 0.06 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com