
ЁОЬтФПЁПвбжЊШчЭМЃЌЁЯCOD=90ЁуЃЌжБЯпABгыOCНЛгкЕуBЃЌгыODНЛгкЕуAЃЌЩфЯпOEКЭЩфЯпAFНЛгкЕуGЃЎ

ЃЈ1ЃЉШєOEЦНЗжЁЯBOAЃЌAFЦНЗжЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЃЈ2ЃЉШєЁЯGOA=![]() ЁЯBOAЃЌЁЯGAD=
ЁЯBOAЃЌЁЯGAD=![]() ЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЁАЁЯOBA=30ЁуЁБИФЮЊЁАЁЯOBA=ІСЁБЃЌЦфгрЬѕМўВЛБфЃЌдђЁЯOGA= ЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ4ЃЉШєOEНЋЁЯBOAЗжГЩ1ЃК2СНВПЗжЃЌAFЦНЗжЁЯBADЃЌЁЯABO=ІСЃЈ30ЁуЃМІСЃМ90ЁуЃЉЃЌЧѓЁЯOGAЕФЖШЪ§ЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉ15ЁуЃЛЃЈ2ЃЉ10ЁуЃЛЃЈ3ЃЉ![]() ІСЃЛЃЈ4ЃЉ
ІСЃЛЃЈ4ЃЉ![]() ІС+15ЁуЛђ
ІС+15ЁуЛђ![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩгкЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌгЩAFЦНЗжЁЯBADЕУЕНЁЯFAD=![]() ЁЯBADЃЌЖјЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ2ЁС45Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=
ЁЯBADЃЌЖјЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ2ЁС45Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуМДПЩЃЛ
ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуМДПЩЃЛ
ЃЈ2ЃЉгЩгкЁЯGOA=![]() ЁЯBOA=30ЁуЃЌЁЯGAD=
ЁЯBOA=30ЁуЃЌЁЯGAD=![]() ЁЯBADЃЌЁЯOBA=ІСЃЌИљОнЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН3ЁС30Ёу+3ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=
ЁЯBADЃЌЁЯOBA=ІСЃЌИљОнЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН3ЁС30Ёу+3ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуЃЛ
ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕУЕНЁЯOGA=![]() ІСЃЛ
ІСЃЛ
ЃЈ4ЃЉЬжТлЃКЕБЁЯEODЃКЁЯCOE=1ЃК2ЪБЃЌРћгУЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН2ЁС30Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІС+15ЁуЃЛ
ІС+15ЁуЃЛ
ЕБЁЯEODЃКЁЯCOE=2ЃК1ЪБЃЌдђЁЯEOD=60ЁуЃЌЭЌРэЕУЁЯOGA=![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ15ЁуЃЛ
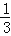
ЃЈ2ЃЉ10ЁуЃЛ
ЃЈ3ЃЉ![]() ІСЃЛ
ІСЃЛ
ЃЈ4ЃЉЕБЁЯEODЃКЁЯCOE=1ЃК2ЪБЃЌ
дђЁЯEOD=30ЁуЃЌ
ЁпЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌ
ЖјAFЦНЗжЁЯBADЃЌ
ЁрЁЯFAD=![]() ЁЯBADЃЌ
ЁЯBADЃЌ
ЁпЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ
Ёр2ЁС30Ёу+2ЁЯOGA=ІС+90ЁуЃЌ
ЁрЁЯOGA=![]() ІС+15ЁуЃЛ
ІС+15ЁуЃЛ
ЕБЁЯEODЃКЁЯCOE=2ЃК1ЪБЃЌдђЁЯEOD=60ЁуЃЌ
ЭЌРэЕУЕНЁЯOGA=![]() ІС-15ЁуЃЌ
ІС-15ЁуЃЌ
МДЁЯOGAЕФЖШЪ§ЮЊ![]() ІС+15ЁуЛђ
ІС+15ЁуЛђ![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ


 Ъ§бЇАТШќЪюМйЬьЬьСЗФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
Ъ§бЇАТШќЪюМйЬьЬьСЗФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
ФЯДѓНЬИЈЧРЯШЦ№ХмЪюМйЯЮНгНЬГЬФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуPЃЈxЃЌyЃЉЕНxжсЕФОрРыЮЊ2ЃЌЕНyжсЕФОрРыЮЊ3ЃЌЧвx+yЃО0ЃЌxyЃМ0ЃЌдђЕуPЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈЉ2ЃЌ3ЃЉB.ЃЈ2ЃЌ3ЃЉC.ЃЈ3ЃЌЉ2ЃЉD.ЃЈ3ЃЌ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЕуEдкACЕФбгГЄЯпЩЯЃЌЯТСаЬѕМўжаФмХаЖЯABЁЮCDЕФЪЧЃЈ ЃЉ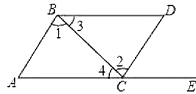
A.ЁЯ3=ЁЯA
B.ЁЯl=ЁЯ2
C.ЁЯD=ЁЯDCE
D.ЁЯD+ЁЯACD=180
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ10ИіВЛЭЌЕФе§ХМЪ§АДЯТЭМХХСаЃЌМ§ЭЗЩЯЗНЕФУПИіЪ§ЖМЕШгкЦфЯТЗНСНЪ§ЕФКЭЃЌШч![]() ЃЌ
ЃЌ![]() БэЪОa1=a2+a3ЃЌдђa1ЕФзюаЁжЕЮЊЃЈ ЃЉ
БэЪОa1=a2+a3ЃЌдђa1ЕФзюаЁжЕЮЊЃЈ ЃЉ

AЃЎ32 BЃЎ36 CЃЎ38 DЃЎ40
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧМзЁЂввЁЂБћШ§ШЫАйУзШќХмЕФКЏЪ§ЭМЯѓЃЌИљОнгвЭМЛиД№ЯТУцЮЪЬтЃЛ
ЃЈ1ЃЉдкетДЮБШШќжаЃЌЛёЕУЙкОќЃК
ЃЈ2ЃЉМзБШввЬсЧАУыЕНДяФПЕФЕиЃЛ
ЃЈ3ЃЉввЕФЫйЖШБШБћПьУз/Уы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.СНУћЭЌбЇ5ДЮЦНОљЗжЯрЭЌЃЌдђЗНВюНЯДѓЕФЭЌбЇГЩМЈИќЮШЖЈ
B.зщЪ§Он3ЃЌ4ЃЌ4ЃЌ6ЃЌ8ЃЌ5ЕФжкЪ§ЮЊ4
C.зщЪ§Он3ЃЌ4ЃЌ4ЃЌ6ЃЌ8ЃЌ5ЕФжаЮЛЪ§ЮЊ4
D.БиШЛЪТМўЕФИХТЪЪЧ100ЃЅЃЎЫцЛњЪТМўЕФИХТЪЪЧ50ЃЅ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
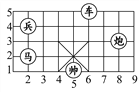
ЁОЬтФПЁПШчЭМЪЧжаЙњЯѓЦхвЛДЮЖдОжЪБЕФВПЗжЪОвтЭМЃЌШєЁАЫЇЁБЫљдкЕФЮЛжУгУгаађЪ§Жд(5ЃЌ1)БэЪОЃЎ
(1)ЧыФугУгаађЪ§ЖдБэЪОЦфЫћЦхзгЕФЮЛжУЃЛ
(2)ЮвУЧжЊЕРТэааЁАШеЁБзжЃЌШчЭМжаЕФЁАТэЁБЯТвЛВНПЩвдзпЕН(3ЃЌ4)ЕФЮЛжУЃЌЮЪЛЙПЩвдзпЕФЮЛжУгаМИИіЃПЗжБ№ШчКЮБэЪОЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДгЯТСаЫФИіЬѕМўЃКЂйBCЃНBЁфCЃЛЂкACЃНAЁфCЃЛЂлЁЯAЁфCAЃНЁЯBЁфCBЃЛЂмABЃНAЁфBЁфжаЃЌШЮШЁШ§ИіЮЊЬѕМўЃЌгрЯТЕФвЛИіЮЊНсТлЃЌдђзюЖрПЩвдЙЙГЩе§ШЗЕФНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
A.1
B.2
C.3
D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊгаРэЪ§aЁЂbТњзуЃЈa+2ЃЉ2+|2bЉ6|ЃН0ЃЌдђaЉbЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com