【题目】已知点P（x，y）到x轴的距离为2，到y轴的距离为3，且x+y＞0，xy＜0，则点P的坐标为（ ）
A.（﹣2，3）B.（2，3）C.（3，﹣2）D.（3，2）
科目：初中数学 来源： 题型：
【题目】下列哪一个是假命题（ ）
A.五边形外角和为360°B.圆的切线垂直于经过切点的半径
C.(3，﹣2)关于y轴的对称点为(﹣3，2)D.抛物线y＝x2﹣4x+2017对称轴为直线x＝2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂在A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为6000元，使用B型车厢每节费用为8000元.
（1）设运送这批货物的总费用为y万元，这列货车挂A型车厢x 节，试定出用车厢节数x表示总费用y的公式.
（2）如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
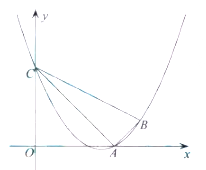
【题目】如图，已知二次函数
的图象经过点
，
，且与
轴交于点
，连接
、
、
.
(1)求此二次函数的关系式；
(2)判断
的形状；若
的外接圆记为
，请直接写出圆心
的坐标；
(3)若将抛物线沿射线
方向平移，平移后点
、
、
的对应点分别记为点
、
、
，
的外接圆记为
，是否存在某个位置，使经过原点？若存在，求出此时抛物线的关系式；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列调查方式，你认为最合适的是（ ）
A.了解某地区饮用水矿物质含量的情况，采用抽样调查方式
B.旅客上飞机前的安检，采用抽样调查方式
C.调查某种品牌笔芯的使用寿命，采用全面调查方式
D.调查浙江卫视《奔跑吧，兄弟》节目的收视率，采用全面调查方式
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
市首批一次性投放公共自行车700辆供市民租用出行，由于投入数量不够， 导致出现需要租用却未租到车的现象，现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7：00﹣8：00 | 第二天7：00﹣8：00 | 第三天7：00﹣8：00 | 第四天7：00﹣8：00 | 第五天7：00﹣8：00 |
需要租用自行车却未租到车的人数（人） | 1500 | 1200 | 1300 | 1300 | 1200 |
（1）表格中的五个数据（人数）的中位数是多少？
（2）由随机抽样估计，平均每天在7:00-8:00 :需要租用公共自行车的人数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．
（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=30°，则∠OGA= .
（2）若∠GOA=
∠BOA，∠GAD=∠BAD，∠OBA=30°，则∠OGA= .
（3）将（2）中“∠OBA=30°”改为“∠OBA=α”，其余条件不变，则∠OGA= （用含α的代数式表示）
（4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO=α（30°＜α＜90°），求∠OGA的度数（用含α的代数式表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
