
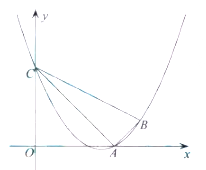
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)求此二次函数的关系式;
(2)判断![]() 的形状;若
的形状;若![]() 的外接圆记为
的外接圆记为![]() ,请直接写出圆心
,请直接写出圆心![]() 的坐标;
的坐标;
(3)若将抛物线沿射线![]() 方向平移,平移后点
方向平移,平移后点![]() 、
、![]() 、
、![]() 的对应点分别记为点
的对应点分别记为点![]() 、
、![]() 、
、![]() ,
,![]() 的外接圆记为
的外接圆记为![]() ,是否存在某个位置,使
,是否存在某个位置,使![]() 经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
【答案】(1)![]() (2)直角三角形,(2,2)(3)存在,抛物线的关系式为
(2)直角三角形,(2,2)(3)存在,抛物线的关系式为
![]() 或
或![]()
【解析】
试题分析:(1)根据待定系数法可直接代入得到方程组求值,得到函数的解析式;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,然后根据角之间的关系得到是直角三角形,最后根据坐标得到D点;
,然后根据角之间的关系得到是直角三角形,最后根据坐标得到D点;
(3)取![]() 中点
中点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据勾股定理求出MC的长和OM的长,再通过平移的性质得到平移的距离,然后根据二次函数的平移性质可得到解析式.
,根据勾股定理求出MC的长和OM的长,再通过平移的性质得到平移的距离,然后根据二次函数的平移性质可得到解析式.
试题解析:(1)把点![]() ,
,![]() 代入
代入![]() 中得
中得
![]() ,解得
,解得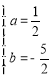 ,
,
所以所求函数的关系式为![]() .
.
(2)![]() 为直角三角形.
为直角三角形.
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
易知点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为点![]() 坐标为
坐标为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 为直角三角形,
为直角三角形,
圆心![]() 的坐标为
的坐标为![]() .
.
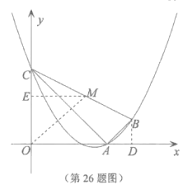
(3)存在.
取![]() 中点
中点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
因为![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以要使抛物线沿射线![]() 方向平移,
方向平移,
且使![]() 经过原点,
经过原点,
则平移的长度为![]() 或
或![]() ,
,
因为![]() ,
,
所以抛物线的顶点向左、向下均分别平移![]() 个单位长度,
个单位长度,
或![]() 个单位长度.
个单位长度.
因为![]() .
.
所以平移后抛物线的关系式为![]() ,
,
即![]()
或![]() ,即
,即![]() .
.
综上所述,存在一个位置,使![]() 经过原点,此时抛物线的关系式为
经过原点,此时抛物线的关系式为
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
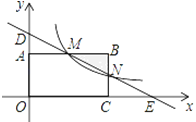
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y=![]() (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
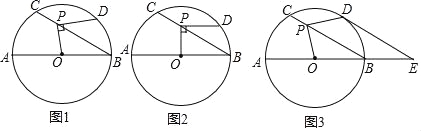
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为![]() 分(
分(![]() ).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
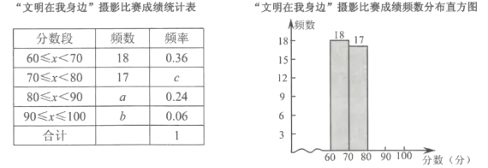
根据以上信息解答下列问题:
(1)统计表中![]() 的值为 ;样本成绩的中位数落在分数段 中;
的值为 ;样本成绩的中位数落在分数段 中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x,y)到x轴的距离为2,到y轴的距离为3,且x+y>0,xy<0,则点P的坐标为( )
A.(﹣2,3)B.(2,3)C.(3,﹣2)D.(3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(黄石中考)一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表所示,现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销互动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为_______元.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如![]() ,
,![]() 表示a1=a2+a3,则a1的最小值为( )
表示a1=a2+a3,则a1的最小值为( )

A.32 B.36 C.38 D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com