
【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如![]() ,
,![]() 表示a1=a2+a3,则a1的最小值为( )
表示a1=a2+a3,则a1的最小值为( )

A.32 B.36 C.38 D.40
【答案】D.
【解析】
试题分析:由a1=a7+3(a8+a9)+a10知要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,根据a5=a8+a9=6,则a7、a10中不能有6,据此对于a7、a8,分别取8、10、12检验可得.
∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3(a8+a9)+a10,
∴要使a1取得最小值,则a8+a9应尽可能的小,取a8=2、a9=4,∵a5=a8+a9=6,则a7、a10中不能有6,
若a7=8、a10=10,则a4=10=a10,不符合题意,舍去;若a7=10、a10=8,则a4=12、a6=4+8=12,不符合题意,舍去;若a7=10、a10=12,则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40,符合题意;
综上,a1的最小值为40,
故选:D.


科目:初中数学 来源: 题型:
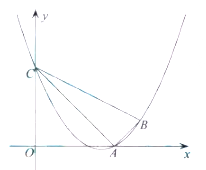
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)求此二次函数的关系式;
(2)判断![]() 的形状;若
的形状;若![]() 的外接圆记为
的外接圆记为![]() ,请直接写出圆心
,请直接写出圆心![]() 的坐标;
的坐标;
(3)若将抛物线沿射线![]() 方向平移,平移后点
方向平移,平移后点![]() 、
、![]() 、
、![]() 的对应点分别记为点
的对应点分别记为点![]() 、
、![]() 、
、![]() ,
,![]() 的外接圆记为
的外接圆记为![]() ,是否存在某个位置,使
,是否存在某个位置,使![]() 经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“和谐号”火车从车站出发,在行驶过程中速度![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )的关系如图所示,其中线段
)的关系如图所示,其中线段![]() 轴.
轴.
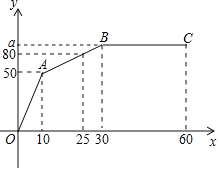
(1)当![]() ,求
,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若现有长为3cm,4cm,7cm,9cm的四根木棒,任取其中三根组成一个三角形,则可以组成不同的三角形的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.

(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA= .
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA= .
∠BAD,∠OBA=30°,则∠OGA= .
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com