
科目:初中数学 来源: 题型:填空题
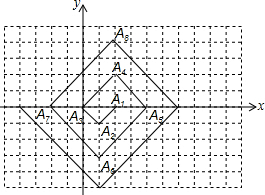 如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).
如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在三个偶数中任选一个能被2整除 | |
| B. | 两个有理数相除,结果是无理数 | |
| C. | 一个四边形的内角和是560° | |
| D. | 用一个平面去截圆柱体,得到的截面是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
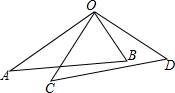 如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的等于( )
如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的等于( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
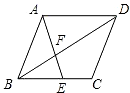 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com