
【题目】如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
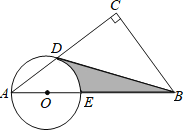
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,DE,求出∠ADE=90°=∠C,推出DE∥BC,求出∠EDB=∠CBD=∠A,根据∠A+∠OED=90°,求出∠EDB+∠ODE=90°,根据切线的判定推出即可;
(2)分别求出扇形DOE和△ODB的面积,即可求出答案.
解:(1)直线BD与⊙O的位置关系是相切
证明:连接OD、DE

∵∠C=90°
∴∠CBD+∠CDB=90°
∵∠A=∠CBD
∴∠A+∠CDB=90°
∵OD=OA
∴∠A=∠ADO
∴∠ADO+∠CDB=90°
∴∠ODB=180°﹣90°=90°
∴OD⊥BD
∵OD为半径
∴BD是⊙O切线
(2)解:∵AE是⊙O直径
∴∠ADE=90°
∵AE=4,∠A=30°
∴DE=![]() AE=2,∠AED=60°
AE=2,∠AED=60°
∵OD=OE
∴△DOE是等边三角形
∴∠ODE=60°,OD=OE=DE=2
∵∠ODB=90°
∴∠EDB=30°
∴∠B=∠DEO﹣∠EDB=60°﹣30°=30°
∴OB=2OD=4
由勾股定理得:DB=![]() ,
,
∴阴影部分的面积S=S△ODB﹣S扇形DOE
=![]()
=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 交边
交边![]() 于点
于点![]() .
.

(1)当点![]() 与
与![]() 恰好重合时(如图1),求
恰好重合时(如图1),求![]() 的长;
的长;
(2)问:是否可能使![]() 、
、![]() 与
与![]() 都相似?若能,请求出此时
都相似?若能,请求出此时![]() 的长;若不能,请说明理由(如图2).
的长;若不能,请说明理由(如图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
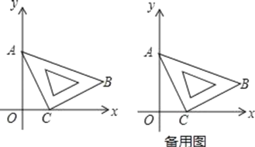
(1)直接写出点B的坐标是 ;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
(4)在x轴上方,抛物线l上是否存在一点P,使由点A,C,B,P构成的四边形为中心对称图形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的![]() ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为![]() ?若存在,
?若存在,
求出运动所需的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁迅猛发展,给我们的出行带来极大的便捷,如图1,是某种新设计动车车头的纵截面一部分,曲线OBA是一开口向左,对称轴正好是水平线OC的抛物线的一部分,点A、B是车头玻璃罩的最高点和最低点,AC、BD是两点到车厢底部的距离,OD=1.5米,BD=1.5米,AC=3米,请你利用所学的函数知识解决以下问题.
(1)为了方便研究问题,需要把曲线OBA绕点O旋转转化为我们熟悉的函数,请你在所给的方框内,画出你旋转后函数图象的草图,在图中标出点O、A、B、C、D对应的位置,并求你所画的函数的解析式.
(2)如图2,驾驶员座椅安装在水平线OC上一点P处,实验表明:当PA+PB最小时,驾驶员驾驶时视野最佳,为了达到最佳视野,求OP的长.
(3)驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑,一个驾驶员坐下时头顶到椅面的距离为1米,在(2)的情况下,座椅最多条件到多少时他才感到舒适?

查看答案和解析>>
科目:初中数学 来源: 题型:
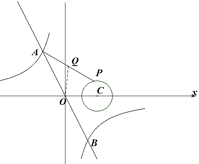
【题目】如图,一次函数y=-2x与反比例函数y=![]() (k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为
(k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
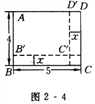
【题目】如图2 - 4所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
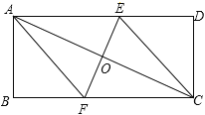
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,EF=6,求菱形AFCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com