
����Ŀ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ壨��ABC������ͼ��ʾ���ã���AO��2��OC��1����ACB��90�㣮
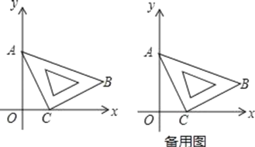
��1��ֱ��д����B���������� ��
��2�����������l��y��ax2��ax��2������B������������l�Ľ���ʽ��
��3���ѡ�ABC���ŵ�C��ʱ����ת90�����A�Ķ�Ӧ��A1�Ƿ���������l�ϣ�Ϊʲô��
��4����x���Ϸ���������l���Ƿ����һ��P��ʹ�ɵ�A��C��B��P���ɵ��ı���Ϊ���ĶԳ�ͼ�Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1����B������Ϊ��3��1������2��y��![]() x2��
x2��![]() x��2����3����A1���������ϣ����ɼ���������4�����ڣ���P����2��1����
x��2����3����A1���������ϣ����ɼ���������4�����ڣ���P����2��1����
��������
��1����������B��BD��x�ᣬ����ΪD��ͨ��֤����BDC�ա�COA���ɵ�BD��OC��1��CD��OA��2���Ӷ���֪B���ꣻ
��2�����ô���ϵ��������B������뼴����ã�
��3��������ת���ͼ�Σ�����![]() ��x��Ĵ��ߣ�����ȫ�������Σ����
��x��Ĵ��ߣ�����ȫ�������Σ����![]() ��������������߽���ʽ���ɽ����жϣ�
��������������߽���ʽ���ɽ����жϣ�
��4���������ߵĽ���ʽ�����P�����꣬�ٸ������ĶԳƵ����� ���߶��е�Ĺ�ʽ�г�������⼴�ɡ�
��1����ͼ1������B��BD��x�ᣬ����ΪD��
�ߡ�BCD+��ACO��90�㣬��AC0+��OAC��90�㣬
���BCD����CAO��
�֡ߡ�BDC����COA��90�㣬CB��AC��
�ڡ�BDC�͡�COA�У�
�ߡ�BDC=��COA����BCD����CAO��CB=AC��
���BDC�ա�COA��AAS����
��BD��OC��1��CD��OA��2��
���B��������3��1����
��2����������y��ax2��ax��2����B��3��1����
��1��9a��3a��2��
��ã�a��![]() ��
��
�������ߵĽ���ʽΪy��![]() x2��
x2��![]() x��2��
x��2��
��3����ת����ͼ1��ʾ������A1��A1M��x�ᣬ
�߰ѡ�ABC���ŵ�C��ʱ����ת90�㣬
���ABC����A1BC��90�㣬
��A1��B��C���ߣ�
��������BDC��������A1CM��
�ߡ�BDC=��A1MC=90������BCD=��A1CM��A1C=BC,
���BDC�ա�A1CM
��CM��CD��3��1��2��A1M��BD��1��
��OM��1��
���A1����1����1����
�ѵ�x����1����y��![]() x2��
x2��![]() x��2��
x��2��
y����1��
���A1���������ϣ�
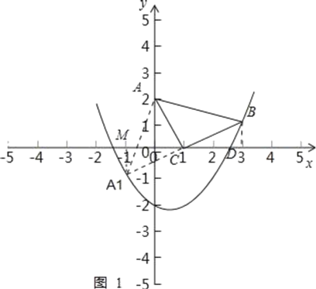
��4�����P��t��![]() t2��
t2��![]() t��2����
t��2����
��A��0��2������C��1��0������B��3��1����
����P�͵�C��Ӧ�������ĶԳƵ����ʺ��߶��е㹫ʽ�ɵã�
![]() ��
��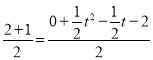 ��
��
�⣬
����P�͵�A��Ӧ�������ĶԳƵ����ʺ��߶��е㹫ʽ�ɵã�
![]() ��
��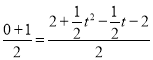 ��
��
�⣬
����P�͵�B��Ӧ�������ĶԳƵ����ʺ��߶��е㹫ʽ�ɵã�
![]() ��
��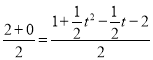 ��
��
��ã�t����2��
![]() t2��
t2��![]() t��2��1
t��2��1
���ԣ����ڣ���P����2��1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����̽��
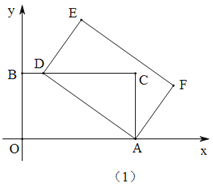
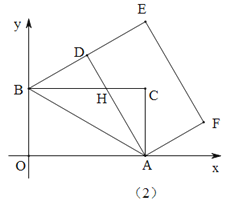
��ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���![]() (0,0)����A(5,0)����B(0,3).�Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD,E��F.
(0,0)����A(5,0)����B(0,3).�Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD,E��F.
(1)��ͼ(1)������D����BC����ʱ�����D�����ꣻ
(2)��ͼ(2)������D�����߶�BE��ʱ��AD��BC���ڵ�H.
����֤����ADB����AOB��
�����H������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
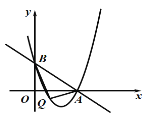
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() �������߾���
�������߾���![]() ��
��![]() ���㣬�ҶԳ���Ϊֱ��
���㣬�ҶԳ���Ϊֱ��![]() .
.
��1���������ߵı���ʽ��
��2�������![]() �������������
������������λ��![]() ���·���һ�㣬�ҡ�
���·���һ�㣬�ҡ�![]() �������
�������![]() .���
.���![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������min{a��b}�ĺ���Ϊ����a��bʱ��min{a��b}=b����a��bʱ��min{a��b}=a���磺min{1��-2��=-2��min{-3��-2��=-3����min{x��-x}=x2-1�Ľ���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1��A��P��B��C�ǡ�O�ϵ��ĸ��㣮��APC=��CPB=60����
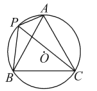
��1���ж���ABC����״�� ��
��2����̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
��3������Pλ��![]() ��ʲôλ��ʱ���ı���APBC�������������������
��ʲôλ��ʱ���ı���APBC�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĶ�������Ϊ��2��1�����Ҿ����㣨-1��-8����
��1����������ߵĺ�������ʽ��
��2������������������Ľ������ꣻ
��3�����Ա���x��ȡֵ��Χ��![]() �����Ӧ�ĺ���ֵy��ȡֵ��Χ��
�����Ӧ�ĺ���ֵy��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
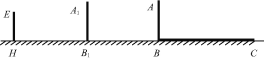
����Ŀ��ѧϰͶӰ��,С����Сӱ���õƹ����Լ���Ӱ�ӳ���������һ·�Ƶĸ߶�,��̽��Ӱ�ӳ��ȵı仯����.��ͼ,��ͬһʱ��,����Ϊ1.6 m��С��(AB)��Ӱ��BC����3 m,��Сӱ(EH)�պ���·�Ƶ��ݵ����·�H��,�����HB=6 m.
(1)����ͼ�л����γ�Ӱ�ӵĹ���,��ȷ��·�Ƶ������ڵ�λ��G;
(2)��·�Ƶ��ݵĴ�ֱ�߶�GH;
(3)���С�����߶�BH��Сӱ(��H)��ȥ,��С���ߵ�BH���е�B1��ʱ,��Ӱ�ӳ�ΪB1C1;��С��������ʣ��·�̵�![]() ��B2��ʱ,��Ӱ�ӳ�ΪB2C2;��С��������ʣ��·�̵�
��B2��ʱ,��Ӱ�ӳ�ΪB2C2;��С��������ʣ��·�̵�![]() ��B3��,��,���˹��ɼ�������ȥ,��С����ʣ��·�̵�
��B3��,��,���˹��ɼ�������ȥ,��С����ʣ��·�̵�![]() ��Bn��ʱ,��Ӱ��BnCn�ij�Ϊ
��Bn��ʱ,��Ӱ��BnCn�ij�Ϊ![]() ��m.(ֱ���ú�n�Ĵ���ʽ��ʾ)
��m.(ֱ���ú�n�Ĵ���ʽ��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���C��90������D��AC�ϣ���CBD����A����A��D�����Բ��Բ��O��AB��.
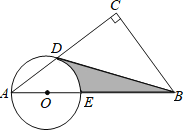
��1���ж�BD����ֱ�����O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����AE��4����A��30������ͼ����BD��BE����DEΧ����Ӱ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
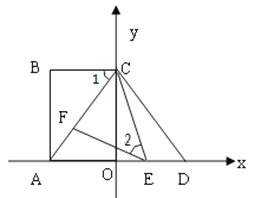
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᡢy���ϣ��ı���ABCOΪ���Σ�AB=16����D���A����y��Գƣ�AB��BC=4��3����E��F�ֱ����߶�AD��AC�ϵĶ��㣨��E�����A��D�غϣ�������1=��2��
��1����AC�ij��͵�D�����ꣻ
��2����֤����AEF����DCE��
��3������EFCΪ����������ʱ�����E�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com