
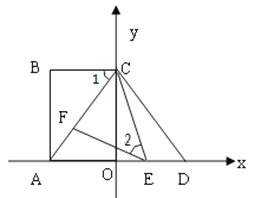
【题目】如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,AB:BC=4:3,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠1=∠2.
(1)求AC的长和点D的坐标;
(2)求证:△AEF∽△DCE;
(3)当△EFC为等腰三角形时,求点E的坐标.
【答案】(1)AC=20,D的坐标为(12,0);(2)证明见解析;(3)E(8,0)或E(![]() ,0).
,0).
【解析】
(1)由tan∠ACB的值,求出cos∠ACB的值,再由矩形ABCO,以及AB的长,求出BC与AC的长,利用对称性确定出D坐标即可;
(2)由对称性得到∠CDE=∠CAO,利用等式的性质得到一对角相等,利用两角相等的三角形相似即可得证;
(3)当△EFC为等腰三角形时,有以下三种情况:当CE=EF;当EF=FC;当CE=CF时,利用相似三角形的判定与性质分别求出E坐标即可.
(1)由题意tan∠ACB=![]() ,
,
∴cos∠ACB=![]() ,
,
∵四边形ABCO为矩形,AB=16,
∴BC=![]() =20,
=20,
∴A(-12,0),
∵点D与点A关于y轴对称,
∴D(12,0);
(2)∵点D与点A关于y轴对称,
∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE,
∴∠AEF=∠DCE,
∴△AEF∽△DCE;
(3)当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
∴△AEF≌△DCE,
∴AE=CD=20,
∴OE=AE-OA=20-12=8,
∴E(8,0);
②当EF=FC时,过点F作FM⊥CE于M,则点M为CE中点,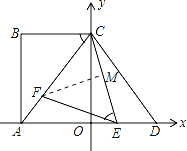
∴CE=2ME=2EFcos∠CEF=2EFcos∠ACB=![]() EF,
EF,
∵△AEF∽△DCE,
∴![]() ,即
,即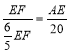 ,
,
∴AE=![]() ,
,
∴DE=AE-OA=![]() ,
,
∴E(![]() ,0);
,0);
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=CAO,即此时点E与点D重合,这与已知条件矛盾,
综上所述,E(8,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
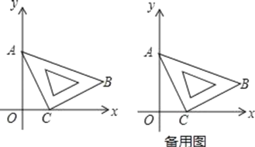
(1)直接写出点B的坐标是 ;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
(4)在x轴上方,抛物线l上是否存在一点P,使由点A,C,B,P构成的四边形为中心对称图形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
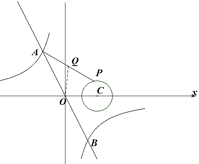
【题目】如图,一次函数y=-2x与反比例函数y=![]() (k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为
(k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
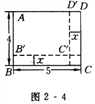
【题目】如图2 - 4所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
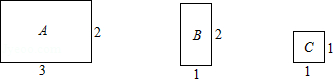
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AB=BC,∠B=∠C=90°,P是BC边上一点,AP⊥PD,E是AB边上一点,∠BPE=∠BAP.
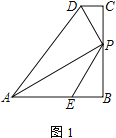
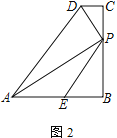
(1) 如图1,若AE=PE,直接写出![]() =______;
=______;
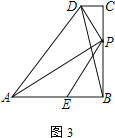
(2) 如图2,求证:AP=PD+PE;
(3) 如图3,当AE=BP时,连BD,则![]() =______,并说明理由.
=______,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
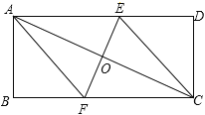
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,EF=6,求菱形AFCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
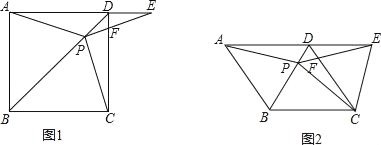
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com