
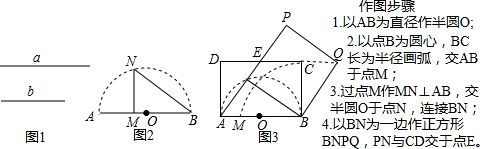
分析 (1)利用圆周角定理和相似三角形的判定及性质易得结论;
(2)①结合图形,利用(1)的结论和矩形的面积公式易得矩形和正方形的面积相等,由全等三角形的判定可得△ADE对应△BCQ,△ABN对应△EQP;
②由其推理过程易得矩形ABCD最少可被分成4块拼合成正方形BNPQ;
③由②的推理过程和(1)的结论得结果.
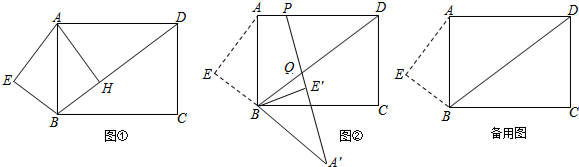
解答 (1)证明:连接AN,如图①,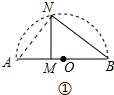
∵AB为半圆O的直径,
∴∠ANB=90°,
∵MN⊥AB,
∴∠NMB=90°,
∴∠ANB=∠NMB,
又∠B为公共角,
∴△ANB∽△NMB,
∴$\frac{AB}{BN}=\frac{BN}{BM}$,
∴BN2=AB•BM=ab,
即BN=$\sqrt{ab}$;
(2)解:①∵S正方形BNPQ=BN2,
由(1)可知BN=$\sqrt{ab}$,
∴S正方形BNPQ=ab,
又∵S矩形ABCD=AB•BC=ab,
∴S正方形BNPQ=S矩形ABCD,
∵$\left\{\begin{array}{l}{AD=BC}\\{∠ADE=∠BCQ}\\{∠AED=∠BQC}\end{array}\right.$,
∴△ADE≌△BQC,
故△ADE对应△BCQ,△ABN对应△EQP,
故答案为:△BCQ,△EQP;
②答案为:4;
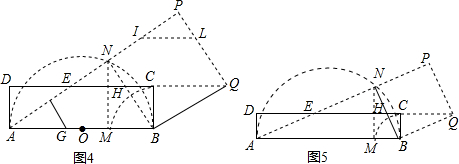
③如图②所示,
剪拼线为IJ、FG,KL、RS,
其中,FG∥IJ∥BN,且BJ=JG=HQ;RS∥KL∥DQ,且SL=LQ=BH,
当AN≤3BN时,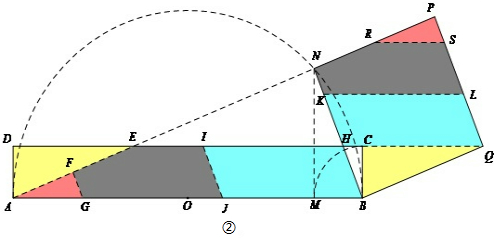 有AN2≤9BN2,
有AN2≤9BN2,
在Rt△ABN中,
有AN2=AB2-BN2,
∴AB2-BN2≤9BN2,
即AB2≤10BN2,
∴a2≤10•$(\sqrt{ab})^{2}$,
化简得 $\frac{a}{b}$≤10,
则$\frac{a}{b}$的最大值为10.
点评 本题主要考查了圆周角定理和相似三角形的性质,利用前面问题得出的结论,数形结合解决问题是解答此题的关键.


科目:初中数学 来源: 题型:填空题
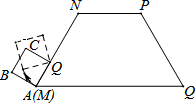 如图,四边形MNPQ中NP∥AQ,NP=2,AN=3,∠Q=60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在四边形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与四边形MNPQ的三边MN、NP、PQ所围成图形的面积S=$\frac{7}{3}$π+2.
如图,四边形MNPQ中NP∥AQ,NP=2,AN=3,∠Q=60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在四边形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与四边形MNPQ的三边MN、NP、PQ所围成图形的面积S=$\frac{7}{3}$π+2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
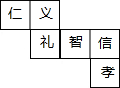 “仁义礼智信孝”是我们中华民族的传统美德,小明同学将这六个字分别写在一个正方体六个表面上,这个正方体的表面展开图如图所示,那么与“孝”所在面相对的面上的字是义.
“仁义礼智信孝”是我们中华民族的传统美德,小明同学将这六个字分别写在一个正方体六个表面上,这个正方体的表面展开图如图所示,那么与“孝”所在面相对的面上的字是义.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
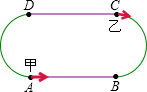 已知甲、乙两人在一个200米的环形跑道上练习跑步,现在把跑道分为相等的4段,即两条直跑道和两条弯道的长度相等.甲平均每秒跑4米,乙平均每秒跑6米.若甲、乙两人分别从A、C两处同时出发(如图),则他们第100次相遇时在跑道( DA )上(填“AB”或“BC”或“DA”或“CD”)
已知甲、乙两人在一个200米的环形跑道上练习跑步,现在把跑道分为相等的4段,即两条直跑道和两条弯道的长度相等.甲平均每秒跑4米,乙平均每秒跑6米.若甲、乙两人分别从A、C两处同时出发(如图),则他们第100次相遇时在跑道( DA )上(填“AB”或“BC”或“DA”或“CD”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com