
【题目】如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
【答案】
(1)
解:如图1,
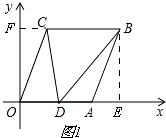
∵A(6,0),B(8,6),
∴FC=AE=8﹣6=2,OF=BE=6
∴C(2,6);
(2)
解:设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴ ![]() ×6x=3×
×6x=3× ![]() ×6(6﹣x),
×6(6﹣x),
∴x= ![]() ,
,
∴D( ![]() ,0);
,0);
若点D在线段OA延长线上,
∵OD=3AD,
∴ ![]() ×6x=3×
×6x=3× ![]() ×6(x﹣6),
×6(x﹣6),
∴x=9,
∴D(9,0)
(3)
解:如图2.
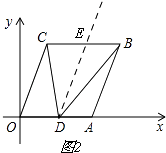
过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE﹣∠EDB=∠OCD﹣∠DBA,
即α﹣β=θ.
【解析】(1)由点的坐标的特点,确定出FC=2,OF=6,得出C(2,6);(2)分点D在线段OA和在OA延长线两种情况进行计算;(3)分点D在线段OA上时,α+β=θ和在OA延长线α﹣β=θ两种情况进行计算;


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:![]() ,ABy轴于B,ACx轴于C
,ABy轴于B,ACx轴于C
(1)求m的值;
(2)如图1,BE=1,过A作AF⊥AE交x轴于F,连EF,D在AO上,且AD=AE,连接ED并延长交x轴于点P,求点P的坐标;
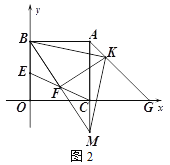
(3)如图2,G为线段OC延长线上一点,AC=CG,E为线段OB上一动点(不与O、B重合),F为线段CE的中点,若BF⊥FK交AG于K,延长BF、AC交于M,连接KM.请问∠FBK的大小是否变化?若不变,请求其值;若改变,求出变化的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学小组的10位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数的2倍加1,第1位同学报( ![]() +1),第2位同学报(
+1),第2位同学报( ![]() +1),第3位同学报(
+1),第3位同学报( ![]() +1)…这样得到的n个数的积为 .
+1)…这样得到的n个数的积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于换季,一家服装店的老板想将某服装打折销售,于是她和正在上七年级的儿子商量打折方案,下面是她和儿子商量时的对话情景:
妈妈:“儿子,每件衣服按标价的5折出售,可以吗?”
儿子:“若每件衣服按标价的5折出售会亏本30元.”
妈妈:“那每件衣服按标价的8折出售呢?”
儿子:“若每件衣服按标价的8折出售将会赚60元.”
……
请根据上面的信息,解决问题:
(1)求这种服装的标价.
(2)若要不亏本,至少打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 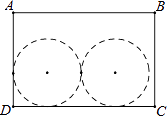
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸片的一角斜折过去,顶点A落在A′处,BC为折痕,再将BE翻折过去与BA′重合,BD为折痕,那么两条折痕的夹角∠CBD=度. 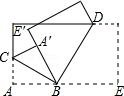
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在第一象限,顶点
在第一象限,顶点![]() 、
、![]() 分别在函数
分别在函数![]() 图像的两个分支上,且
图像的两个分支上,且![]() 经过原点
经过原点![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() 平分四边形
平分四边形![]() 的面积.
的面积.
(1)证明:![]() :
:
(2)求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2﹣5mx+1(m为常数,m>0),设该函数的图象与y轴交于点A,该图象上的一点B与点A关于该函数图象的对称轴对称.
(1)求点A,B的坐标;
(2)点O为坐标原点,点M为该函数图象的对称轴上一动点,求当M运动到何处时,△MAO的周长最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com