
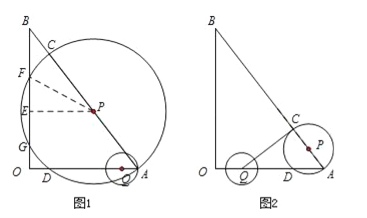
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)0<t≤
;(3)0<t≤![]() 或
或![]() <t≤5.
<t≤5.
【解析】(1)∵OA=6,OB=8,∴由勾股定理可求得:AB=10,由题意知:OQ=AP=t,∴AC=2t,∵AC是⊙P的直径,∴∠CDA=90°,∴CD∥OB,∴△ACD∽△ABO,∴![]() ,∴AD=
,∴AD=![]() ,当Q与D重合时,AD+OQ=OA,∴
,当Q与D重合时,AD+OQ=OA,∴![]() ,∴t=
,∴t=![]() ;
;
(2)当⊙Q经过A点时,如图1,OQ=OA﹣QA=4,∴t=![]() =4s,∴PA=4,∴BP=AB﹣PA=6,过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,连接PF,∴PE∥OA,∴△PEB∽△AOB,∴
=4s,∴PA=4,∴BP=AB﹣PA=6,过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,连接PF,∴PE∥OA,∴△PEB∽△AOB,∴![]() ,∴PE=
,∴PE=![]() ,∴由勾股定理可求得:EF=
,∴由勾股定理可求得:EF=![]() ,由垂径定理可求知:FG=2EF=
,由垂径定理可求知:FG=2EF=![]() ;
;
(3)当QC与⊙P相切时,如图2,此时∠QCA=90°,∵OQ=AP=t,∴AQ=6﹣t,AC=2t,∵∠A=∠A,∠QCA=∠ABO,∴△AQC∽△ABO,∴![]() ,∴
,∴![]() ,∴t=
,∴t=![]() ,∴当0<t≤
,∴当0<t≤![]() 时,⊙P与QC只有一个交点;
时,⊙P与QC只有一个交点;
当QC⊥OA时,此时Q与D重合,由(1)可知:t=![]() ,∴当
,∴当![]() <t≤5时,⊙P与QC只有一个交点,综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤
<t≤5时,⊙P与QC只有一个交点,综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤![]() 或
或![]() <t≤5.
<t≤5.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( ) 
A.(0,0)
B.(0,1)
C.(0,2)
D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( ) 
A.35°
B.45°
C.55°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD. 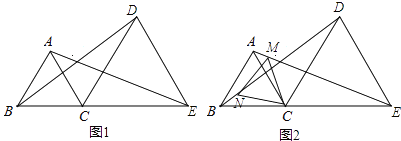
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N. 
(1)若∠ABC=70°,则∠MNA的度数是 .
(2)连接NB,若AB=8cm,△NBC的周长是14cm. ①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com