
【题目】如图,在四边形ABDE中,C是BD边的中点.若AC平分∠BAE,∠ACE=90°,猜想线段AE、AB、DE的长度满足的数量关系为并证明.
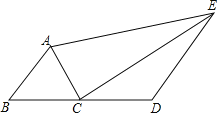
【答案】AE=AB+DE.
【解析】
试题分析:在AE上取一点F,使AF=AB,即可得出△ACB≌△ACF,就可以得出BC=FC,∠ACB=∠ACF,就可以得出△CEF≌△CED.就可以得出结论.
解:AE=AB+DE;
理由:在AE上取一点F,使AF=AB.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
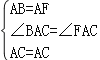 ,
,
∴△ACB≌△ACF(SAS),
∴BC=FC,∠ACB=∠ACF.
∵C是BD边的中点.
∴BC=CD,
∴CF=CD.
∵∠ACE=90°,
∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°
∴∠ECF=∠ECD.
在△CEF和△CED中,
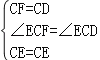 ,
,
∴△CEF≌△CED(SAS),
∴EF=ED.
∵AE=AF+EF,
∴AE=AB+DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
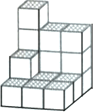
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
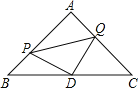
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 小明同学5次数学单元测试的平均成绩是90分,中位数是91分,众数是94分,则两次最低成绩之和是( )
A. 165分 B. 168分 C. 170分 D. 171分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.
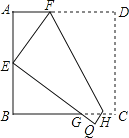
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】82m×4n÷2m﹣n
(2)6m362m÷63m﹣2
(3)(a4a3÷a2)3
(4)(﹣10)2+(﹣10)0+10﹣2×(﹣102)
(5)(![]() x6y5+
x6y5+![]() x5y4﹣
x5y4﹣![]() x4y3)÷
x4y3)÷![]() x3y3
x3y3
(6)![]() x﹣(2x﹣
x﹣(2x﹣![]() y2)+(
y2)+(![]() x﹣
x﹣![]() y2)
y2)
(7)2﹣[x﹣![]() (x﹣1)]﹣
(x﹣1)]﹣![]() (x﹣1)
(x﹣1)
(8)5xy2﹣{2x2y﹣[3xy2﹣(xy2﹣2x2y)]÷(﹣![]() xy)}.
xy)}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次水灾中,大约有2.5×105个人无家可归,假如一顶帐篷占地100米2,可以放置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多少地方?估计你的学校的操场可安置多少人?要安置这些人,大约需要多少个这样的操场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2![]() 的A处发出,把球看成点,其运行的高度
的A处发出,把球看成点,其运行的高度![]() 与运行的水平距离
与运行的水平距离![]() 满足关系式
满足关系式![]() .已知球网与O点的水平距离为9
.已知球网与O点的水平距离为9![]() ,高度为2.43
,高度为2.43![]() ,球场的边界距O点的水平距离为18
,球场的边界距O点的水平距离为18![]() .
.
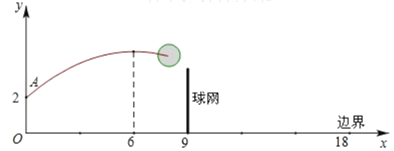
(1)当![]() =2.6时,求
=2.6时,求![]() 与
与![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(2)当![]() =2.6时,球能否越过球网?球会不会出界?请说明理由;
=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求二次函数中![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com