
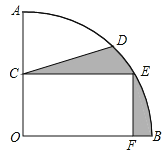
【题目】如图,在扇形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,四边形
上,四边形![]() 是矩形,连接
是矩形,连接![]() .若
.若![]() ,则阴影部分的面积为____________.(结果保留
,则阴影部分的面积为____________.(结果保留![]() )
)
科目:初中数学 来源: 题型:
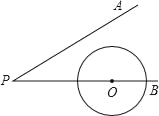
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交点
轴交点![]() ,抛物线
,抛物线![]() 过
过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
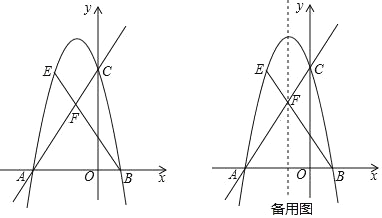
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)在直线![]() 上方的抛物线上是否存在点
上方的抛物线上是否存在点![]() ,使
,使![]() 与
与![]() 的交点
的交点![]() 恰好为
恰好为![]() 的中点?如果存在,求出点
的中点?如果存在,求出点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
(3)若点![]() 在抛物线上且横坐标为
在抛物线上且横坐标为![]() ,点
,点![]() 是抛物线对称轴上一点,在抛物线上存在一点
是抛物线对称轴上一点,在抛物线上存在一点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?直接写出点
为顶点的四边形是平行四边形?直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进了一批商品进行销售,经过一个月的试销发现:该商品的周销售利润![]() (元)与售价
(元)与售价![]() (元/件)满足二次函数关系,这个月的售价、周销售量
(元/件)满足二次函数关系,这个月的售价、周销售量![]() (件)、周销售利润的几组对应值如下表:
(件)、周销售利润的几组对应值如下表:

注:周销售利润=周销售量![]() (售价-进价)
(售价-进价)
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 关于
关于![]() 的函数解析式,该商品每件进价是多少元?
的函数解析式,该商品每件进价是多少元?
(3)该商品打算继续销售这种商品,并希望保持1350元以上的周销售利润,售价应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() 上.
上.
(1)如图1,若抛物线经过点![]() .
.
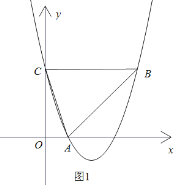
①求抛物线的解析式;
②设抛物线与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,若点
,若点![]() 在抛物线上,且
在抛物线上,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
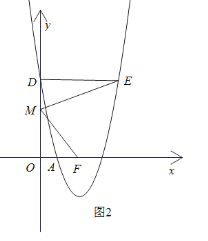
(2)如图2,若抛物线与![]() 轴交于点D过点
轴交于点D过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .点
.点![]() 为抛物线的对称轴与
为抛物线的对称轴与![]() 轴的交点,
轴的交点,![]() 为线段
为线段![]() 上一动点.若以M,D,E为顶点的三角形与
上一动点.若以M,D,E为顶点的三角形与![]() 相似.并且符合条件的点
相似.并且符合条件的点![]() 恰有
恰有![]() 个,请直接写出抛物线的解析式及相应的点
个,请直接写出抛物线的解析式及相应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了部分学生,调查了他们平均每天的睡眠时间(单位:![]() ).以下是根据调查结果绘制的统计图表的一部分.
).以下是根据调查结果绘制的统计图表的一部分.
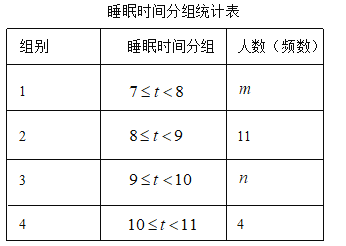
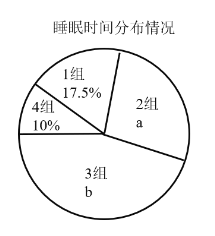
请根据以上信息,解答下列问题:
(1)共随机抽取_______名学生;
(2)![]() _____,
_____,![]() _______,
_______,![]() ______,
______,![]() ______;
______;
(3)抽取的这40名学生平均每天睡眠时间的中位数落在______组(填组别);
(4)如果按照学校要求,学生平均每天的睡眠时间应不少于![]() ,请估计该校学生中睡眠时间符合要求的人数.
,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点四边形ABCD(顶点为网格线的交点).
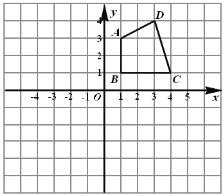
(1)画出四边形ABCD关于x轴成轴对称的四边形A1B1C1D1;
(2)以O为位似中心,在第三象限画出四边形ABCD的位似四边形A2B2C2D2,且位似比为1;
(3)在第一象限内找出格点P,使∠DCP=∠CDP,并写出点P的坐标(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
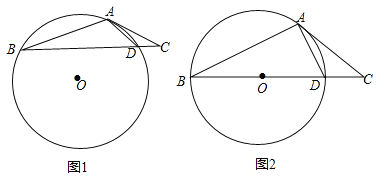
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com