
【题目】某商店进了一批商品进行销售,经过一个月的试销发现:该商品的周销售利润![]() (元)与售价
(元)与售价![]() (元/件)满足二次函数关系,这个月的售价、周销售量
(元/件)满足二次函数关系,这个月的售价、周销售量![]() (件)、周销售利润的几组对应值如下表:
(件)、周销售利润的几组对应值如下表:

注:周销售利润=周销售量![]() (售价-进价)
(售价-进价)
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 关于
关于![]() 的函数解析式,该商品每件进价是多少元?
的函数解析式,该商品每件进价是多少元?
(3)该商品打算继续销售这种商品,并希望保持1350元以上的周销售利润,售价应控制在什么范围内?
【答案】(1)![]() ;(2)
;(2)![]() ,进价为40元;(3)55-85元之间
,进价为40元;(3)55-85元之间
【解析】
(1)本题考查一次函数解析式求法,可用待定系数法求解.
(2)本题考查二次函数与实际利润问题结合,根据题目表格信息分析该二次函数顶点坐标,假设顶点式,继而代入求解二次函数解析式.
(3)本题考查二次函数图形性质的应用,涉及不等式的求法,需结合二次函数对称轴综合判定自变量取值范围.
解:(1)依题意设y=kx+b,把(50,100),(60,80)代入
得![]()
解得![]()
可得y=-2x+200
把(70,60),(80,40)代入均成立
所以y关于x的函数解析式为y=-2x+200
(2)根据题意,二次函数的顶点坐标是(70,1800),设![]() ,把(50,1000)代入,解得a=-2
,把(50,1000)代入,解得a=-2
∴![]()
设进价为m元
根据题意,得(x-m)(-2x+200)=w,将(50,1000)代入
∴m=40
所以每件进价是40元.
(3)根据题意得,-2x2+280x-8000>1350
解得55<x<85
∵a<0,抛物线开口向下,对称轴为直线x=70,
∴55<x<85
所以售价控制在55-85元之间.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
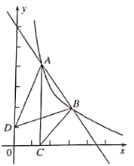
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF,连接CF交线段AB于点G,交AD于点H、连接EG.
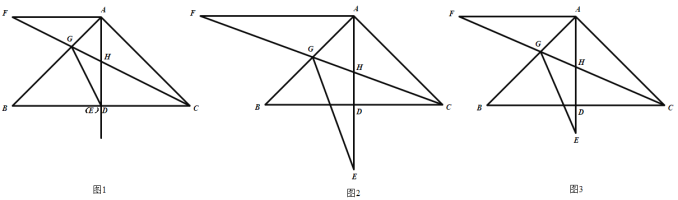
特例分析:
(1)如图1,当点E与点D重合时,“智敏”小组提出如下问题,请你解答:
①求证:AF=CD;
②用等式表示线段CG与EG之间的数量关系为:_______;
拓展探究:
(2)如图2,当点E在线段AD的延长线上,且DE=AD时,“博睿”小组发现CF=2EG.请你证明;
(3)如图3,当点E在线段AD的延长线上,且AE=AB时,![]() 的值为_______;
的值为_______;
推广应用:
(4)当点E在射线AD上运动时,![]() ,则
,则![]() 的值为______用含m.n的式子表示).
的值为______用含m.n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在参加了全市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选科学素养和人文素养的同学分别为![]() 人,
人,![]() 人.”
人.”
小颖:“选数学素养的同学比选阅读素养的同学少![]() 人.”
人.”
小雯:“选科学素养的同学占样本总数的![]() .”
.”
(1)这次抽样调查了多少名学生?
(2)样本总数中,选“阅读素养”、“数学素养”的学生各多少人?
(3)如图是调查结果整理后绘制成的扇形图.请直接在横线上补全相关百分比,并求出“数学素养”所对应的圆心角度数;
(4)该校八年级有学生![]() 人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?
[Failed to download image : blob:http://qbm.xkw.com/61c6a1d7-da76-4939-b41e-e8015f4fdd80]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,“亚洲文明对话大会”在北京成功举办,某研究机构为了了解10-60岁年年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将搜集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第一组 |
| 5 |
第二组 |
|
|
第三组 |
| 35 |
第四组 |
| 20 |
第五组 |
| 15 |
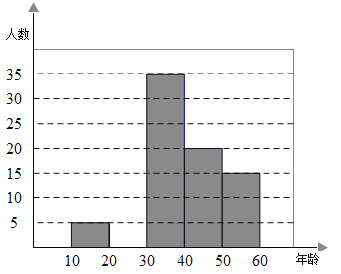

请直接写出第3组人数在扇形统计图中所对应的圆心角是_________度;假设该市现有10-60岁的市民300万人,则40-50岁年龄段的关注本次大会的人数约有___________万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大建设资金的投入.
(1)机场建设项目中所有6个机场投入的建设资金金额统计如下图,已知机场![]() 投入的建设资金金额是机场
投入的建设资金金额是机场![]() 、
、![]() 所投入建设资金金额之和的三分之二,求机场
所投入建设资金金额之和的三分之二,求机场![]() 投入的建设资金金额是多少亿元?并补全条形统计图.
投入的建设资金金额是多少亿元?并补全条形统计图.
(2)将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表,根据扇形统计图及统计表中的信息,求得![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .(请直接填写计算结果)
.(请直接填写计算结果)

铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
投入资金(亿元) | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
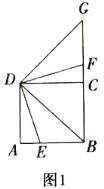
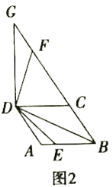
【题目】(1)如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .写出线段
.写出线段![]() ,
,![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
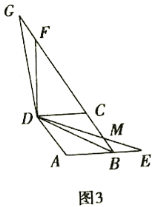
(2)当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() 、
、![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①如图2,点![]() 在线段
在线段![]() 上时,请探究线段
上时,请探究线段![]() ,
,![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
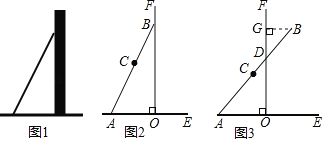
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
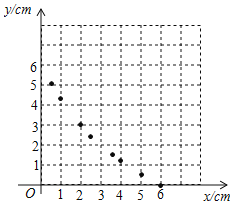
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com