
【题目】如图1.![]() 的半径为
的半径为![]() ,若点
,若点![]() 在射线
在射线![]() 上,且
上,且![]() ,则称点
,则称点![]() 是点
是点![]() 关于
关于![]() 的“反演点”,如图2,
的“反演点”,如图2,![]() 的半径为2,点
的半径为2,点![]() 在
在![]() 上.
上.![]() ,
,![]() ,若点
,若点![]() 是点
是点![]() 关于
关于![]() 的反演点,点
的反演点,点![]() 是点
是点![]() 关于
关于![]() 的反演点,则
的反演点,则![]() 的长为( )
的长为( )
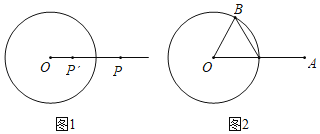
A.![]() B.
B.![]() C.2D.4
C.2D.4
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于y轴对称,点
关于y轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于y轴,直线l的二次对称点.
是点P关于y轴,直线l的二次对称点.
![]() 如图1,点
如图1,点![]() .
.
![]() 若点B是点A关于y轴,直线
若点B是点A关于y轴,直线![]() :
:![]() 的二次对称点,则点B的坐标为______;
的二次对称点,则点B的坐标为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() :
:![]() 的二次对称点,则a的值为______;
的二次对称点,则a的值为______;
![]() 若点
若点![]() 是点A关于y轴,直线
是点A关于y轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为______;
的表达式为______;
![]() 如图2,
如图2,![]() 的半径为
的半径为![]() 若
若![]() 上存在点M,使得点
上存在点M,使得点![]() 是点M关于y轴,直线
是点M关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,b的取值范围是______;
上,b的取值范围是______;
![]() 是x轴上的动点,
是x轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点N,使得点
上存在点N,使得点![]() 是点N关于y轴,直线
是点N关于y轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在y轴上,求t的取值范围.
在y轴上,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
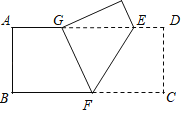
【题目】如图,在长方形纸片ABCD中,AB=3,AD=9,折叠纸片ABCD,使顶点C落在边AD上的点G处,折痕分别交边AD、BC于点E、F,则△GEF的面积最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
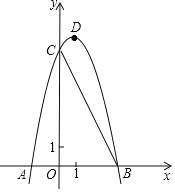
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() .
.
(1)求抛物线的表达式及其顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,将抛物线沿其对称轴向上平移
,将抛物线沿其对称轴向上平移![]() 个单位,使抛物线与线段
个单位,使抛物线与线段![]() (含线段端点)只有1个公共点.求
(含线段端点)只有1个公共点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完成:
(1)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(2)在平面直角坐标系xOy中描出了图象上的一些点,请你画出函数的图象;
下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
y | … | ﹣3.25 | ﹣2.33 | ﹣1.50 | ﹣1 | ﹣1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
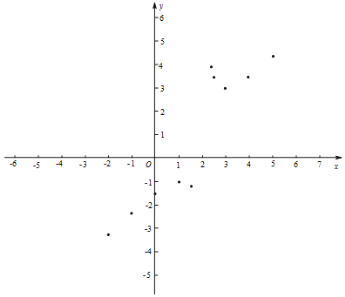
(3)求m的值;
(4)根据图象写出此函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形![]() 为凹四边形.
为凹四边形.
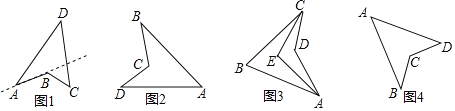
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形![]() 是凹四边形.
是凹四边形.
求证:![]() .
.
(3)性质应用:
如图3,在凹四边形![]() 中,
中,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() °.
°.
(4)类比学习:
如图4,在凹四边形![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,顺次连接各边中点得到四边形
的中点,顺次连接各边中点得到四边形![]() .若
.若![]() ,则四边形
,则四边形![]() 是 .(填写序号即可)
是 .(填写序号即可)
A.梯形 B.菱形 C.矩形 D.正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为线段
为线段![]() 上一点,
上一点,![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
(1)如图1,若![]() ,请补全图形并求
,请补全图形并求![]() 的长;
的长;
(2)如图2,若![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,小明通过观察、实验提出猜想:
,小明通过观察、实验提出猜想:![]() .小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
.小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,先证出
,先证出![]() ,再证出
,再证出![]() 是等腰三角形即可;
是等腰三角形即可;
想法2:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,先证出
,先证出![]() ,再证点
,再证点![]() 为线段
为线段![]() 的中点即可.
的中点即可.
请你参考上面的想法,帮助小明证明![]() .(一种方法即可)
.(一种方法即可)
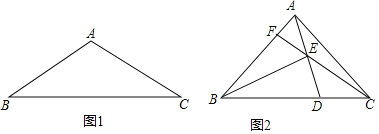
查看答案和解析>>
科目:初中数学 来源: 题型:
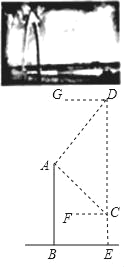
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com