
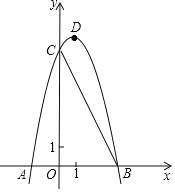
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点,![]() .
.
(1)求抛物线的表达式及其顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
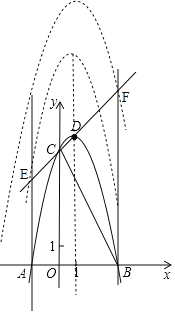
于点![]() ,将抛物线沿其对称轴向上平移
,将抛物线沿其对称轴向上平移![]() 个单位,使抛物线与线段
个单位,使抛物线与线段![]() (含线段端点)只有1个公共点.求
(含线段端点)只有1个公共点.求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;顶点坐标为
;顶点坐标为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 、
、![]() 得点
得点![]() 坐标,将点
坐标,将点![]() 、
、![]() 坐标代入求解可得;
坐标代入求解可得;
(2)先求出直线![]() 解析式和点
解析式和点![]() 、
、![]() 坐标,设平移后解析式为
坐标,设平移后解析式为![]() ,结合图象根据抛物线与线段
,结合图象根据抛物线与线段![]() (含线段端点)只有1个公共点,求得临界时
(含线段端点)只有1个公共点,求得临界时![]() 的值,从而得出答案.
的值,从而得出答案.
(1)由抛物线的表达式知,点![]() ,即
,即![]() ;
;
![]() 中,
中,![]() ,
,
则点![]() .
.
将![]() 、
、![]() 的坐标代入抛物线的表达式中,
的坐标代入抛物线的表达式中,
得:![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为![]() ,
,
∵![]() ,
,
∴抛物线的顶点坐标为![]() .
.
(2)设直线![]() 的表达式为
的表达式为![]() ,
,
∵点![]() ,
,
∴直线![]() 表达式为
表达式为![]() .
.
∵过点![]() 、
、![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() 、
、![]() ,
,
可得:![]() .
.
设抛物线向上平移![]() 个单位长度
个单位长度![]() ,
,
则抛物线的表达式为:![]() ;
;
当抛物线过![]() 时,
时,![]() ,
,
当抛物线过![]() 时,
时,![]() ,
,
∵抛物线与线段![]() (含线段端点)只有1个公共点,
(含线段端点)只有1个公共点,
∴![]() 的取值范围是
的取值范围是![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0),与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.
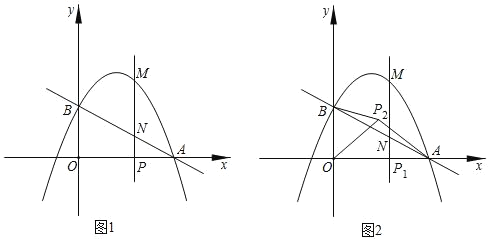
(1)求抛物线的解析式;
(2)若PN:PM=1:4,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
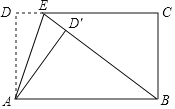
【题目】如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
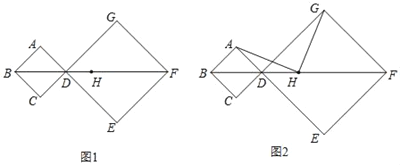
【题目】在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图1,若AB=1,DG=2,求BH的长;
(2)如图2,连接AH,GH.
小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
延庆是全市唯一一个全境域都是水源保护地的区域,森林覆盖率达到57.46%,“干净指数”连续五年全市第一,人均公共绿地面积41.88平方米,空气质量长期保持全市前列.根据区环保局的空气质量的通报,2012年空气质量为优,成为北京市最宜居的地方.
由于经济发展,私家车剧增等原因,2013年空气质量下降为良,尤其是PM2.5平均浓度有所增长,2013年PM2.5平均浓度约为78微克/立方米,比2012年PM2.5平均浓度增长了12.2%.延庆区作为2019年世园会和2022年冬奥会比赛的举办地,将全面治理“煤、气、尘”,逐渐降低PM2.5浓度,力争到2020年降至46微克/立方米,实现“延庆蓝”.
据悉,延庆将大力推广地源热泵、风能、太阳能等新能源和可再生能源.同时强化大货车监管,提升新能源车辆利用率.2020年新能源和可再生能源在延庆的使用比例将达到40%,煤炭能源消费总量占比3%以下,基本建成“无煤区”.
经过全面治理,2014年PM2.5平均浓度约为70微克/立方米,比2013年平均浓度降低了10.26%;2015年PM2.5平均浓度比2014年平均浓度降低了10%,为全市最低;2016年PM2.5平均浓度约为56微克/立方米.
根据以上材料解答下列问题:
(1)2015年PM2.5平均浓度约为 微克/立方米;
(2)选择统计表或统计图,将2013﹣2016年PM2.5平均浓度整理出来;
(3)根据上述材料和绘制的统计表或统计图中提供的信息,预估2017年的PM2.5平均浓度约为 微克/立方米;你的预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.![]() 的半径为
的半径为![]() ,若点
,若点![]() 在射线
在射线![]() 上,且
上,且![]() ,则称点
,则称点![]() 是点
是点![]() 关于
关于![]() 的“反演点”,如图2,
的“反演点”,如图2,![]() 的半径为2,点
的半径为2,点![]() 在
在![]() 上.
上.![]() ,
,![]() ,若点
,若点![]() 是点
是点![]() 关于
关于![]() 的反演点,点
的反演点,点![]() 是点
是点![]() 关于
关于![]() 的反演点,则
的反演点,则![]() 的长为( )
的长为( )
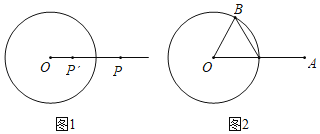
A.![]() B.
B.![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
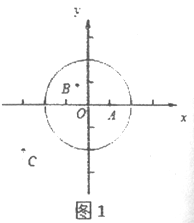
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
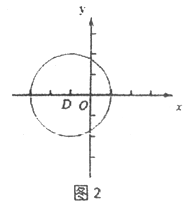
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
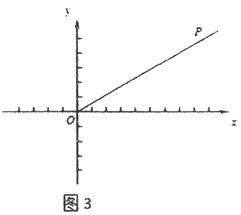
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
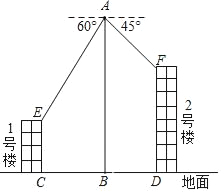
【题目】如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为_____米(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com