
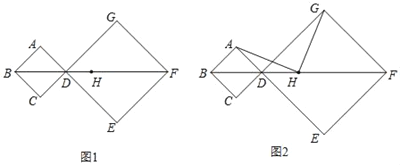
����Ŀ����������ABCD��������DEFG�У�����B��D��F��ͬһֱ���ϣ�H��BF���е㣮
��1����ͼ1����AB=1��DG=2����BH�ij���
��2����ͼ2������AH��GH��
С��۲�ͼ2��������룺AH=GH��AH��GH��С������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1���ӳ�AH��EF�ڵ�M������AG��GM��Ҫ֤�����۳���ֻ��֤��GAM�ǵ���ֱ�������Σ�
�뷨2������AC��GE�ֱ�BF�ڵ�M��N��Ҫ֤�����۳���ֻ��֤��AMH�ա�HNG����
����ο�������뷨������С��֤��AH=GH��AH��GH����һ�ַ������ɣ�
���𰸡���1��![]() ����2��֤��������.
����2��֤��������.
��������
��1���ȸ��ݹ��ɶ����ó�BD��DF���������BF�����ɵó�������
��2���뷨1�����жϡ�ABH�ա�MFH�������жϳ���ADG�ա�MFG�������жϳ���AGMΪ����ֱ�������������ɵó�������
�뷨2�����жϳ�MN=![]() BF�������жϳ���AMH�ա�HNG�������жϳ���AHM+��GHN=90�������ɵó�������
BF�������жϳ���AMH�ա�HNG�������жϳ���AHM+��GHN=90�������ɵó�������
��1������������ABCD��������DEFG�����ABD����GDFΪ����ֱ����������
��AB=1��DG=2�����ɹ��ɶ�����BD=![]() ��DF=2
��DF=2![]() ��
��
��B��D��F��������BF=3![]() ��
��
��H��BF�������BH=![]() BF=
BF=![]() ��
��
��2���뷨1��
��ͼ1���ӳ�AH��EF�ڵ�M������AG��GM��
����������ABCD��������DEFG��B��D��F��������AB��EF�����ABH=��MFH��
�֡�BH=FH����AHB=��MHF�����ABH�ա�MFH����AH=MH��AB=MF��
��AB=AD����AD=MF��
��DG=FG����ADG=��MFG=90�㣬���ADG�ա�MFG�����AGD=��MGF��AG=MG��
�֡ߡ�DGM+��MGF=90�㣬���AGD+��DGM=��AGM=90�㣬���AGMΪ����ֱ����������
��AH=MH����AH=GH��AH��GH��
�뷨2��
��ͼ2������AC��GE�ֱ�BF�ڵ�M��N��
����������ABCD��������DEFG��B��D��F��������AC��BF��GE��BF��DM=AM=![]() BD��DN=GN=
BD��DN=GN=![]() DF�����AMD=��GNH=90�㣬MN=
DF�����AMD=��GNH=90�㣬MN=![]() BF��
BF��
��H��BF�������BH=![]() BF����BH=MN����BH��MH=MN��MH����BM=HN��
BF����BH=MN����BH��MH=MN��MH����BM=HN��
��AM=BM=DM����AM=HN=DM����MD+DH=NH+DH����MH=DN��
��DN=GN����MH=GN��
�ڡ�AMH�͡�HNG�У���AM=HN����AMD=��HNG��MH=NG�����AMH�ա�HNG����AH=GH����AHM=��HGN��
�ߡ�HGN+��GHN=90�㣬���AHM+��GHN=90�㣬���AHG=90�㣬��AH��GH����AH=GH��AH��GH��


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
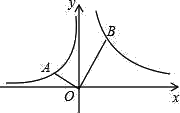
����Ŀ����ͼ��A��B����ֱ��ڷ���������y=![]() ��x��0����y=
��x��0����y=![]() ��x��0����ͼ���ϣ�����OA��OB����OA��OB��OA=
��x��0����ͼ���ϣ�����OA��OB����OA��OB��OA=![]() OB����k��ֵΪ_____��
OB����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��4��0����B��0����2����C��a��a������D��һ��ƽ���ı��ε��ĸ����㣬���߶�CD������СֵΪ___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
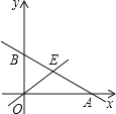
����Ŀ����ͼ��ֱ��y=-![]() x+b��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��y=x���ڵ�E����E�ĺ�����Ϊ3��
x+b��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��y=x���ڵ�E����E�ĺ�����Ϊ3��
��1�����E�������b��ֵ��
��2����x�����е�P��m��0��������P��x��Ĵ��ߣ���ֱ��y=-![]() x+b���ڵ�C����ֱ��y=x���ڵ�D����CD��4����m��ȡֵ��Χ��
x+b���ڵ�C����ֱ��y=x���ڵ�D����CD��4����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC������A����B����C�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������������ж���ABCΪֱ�������ε����� ����
�����������������ж���ABCΪֱ�������ε����� ����
A����A+��B=��C
B����A�á�B�á�C =1��2��3
C��![]()
D��![]() ��
��![]() ��
��![]() =3��4��6
=3��4��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ڼס��Ҳֿ���ij��ԭ��450�֣�����˳��ײֿ�����ԭ�ϵ�60%���Ҳֿ�����ԭ�ϵ�40%����ô�Ҳֿ�ʣ���ԭ�ϱȼײֿ�ʣ���ԭ�϶�30�֣�
��1����ס������ֿ�����ԭ�϶��ٶ֣�
��2���ֹ�˾�轫300��ԭ�������������Ӽס��������ֿ�������˼۷ֱ�Ϊ120Ԫ/�ֺ�100Ԫ/�֣���Э�̣��Ӽײֿ�������˼ۿ��Ż�aԪ�֣�10��a��30�������Ҳֿ�������˼۲��䣬��Ӽײֿ���m��ԭ�ϵ���������������˷�W����m�ĺ�������ʽ����Ҫ��д��m��ȡֵ��Χ����
��3���ڣ�2���������£�����ݺ���������˵��������m������W�ı仯�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������˾Ϊ��������Ϊ����ᡱ�����3000Ԫ����֪��˾���������ҹ�˾��������20%���ҹ�˾�ȼ�˾�˾����20Ԫ���������������Ϣ������������˾�ġ����������˾������һ���÷�ʽ���̽�����⣬��д��������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ y��2 �� x+1 ������������ x��7 ʱ��y��6��
��1��д�� y �� x ֮��ĺ�����ϵʽ��
��2���� y=��2 ʱ���� x ��ֵ��
��3������ P����6,m+4���ڸú���ͼ���ϣ��� m ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲����Ӷ�l1�����ù���A��B֮��ľ��룬ij��ѧ��ȤС���ں����������ABƽ�е�ֱ��l2��ȡC��D���㣬��á�ACB=15�㣬��ACD=45������l1��l2֮��ľ���Ϊ50m����A��B֮��ľ���Ϊ��������
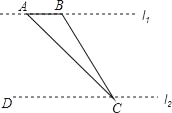
A. 50m B. 25m C. ��50��![]() ��m D. ��50��25
��m D. ��50��25![]() ��m
��m
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com