
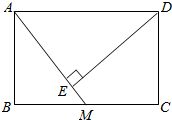
 矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.
矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.分析 (1)根据矩形的性质得∠B=90°,AD∥BC,则∠DAE=∠AMB,而DE⊥AM,所以∠B=∠AED=90°,于是根据相似三角形的判定即可得到△ADE∽△MAB;
(2)由△ADE∽△MAB,可得到AB•AE=DE•MB,又AB=CD,BM=MC,等量代换即可得出结论;
(3)由M是BC中点,AD=BC=6得到BM=3,在Rt△ABM中,根据勾股定理得AM=5,再由△ADE∽△MAB,利用相似比计算出AE,然后利用EM=AM-AE求解
解答 (1)证明:∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,
∴∠DAE=∠AMB,
∵DE⊥AM
∴∠B=∠AED=90°,
∴△ADE∽△MAB;
(2)∵△ADE∽△MAB,
∴AB•AE=DE•MB,
∵四边形ABCD为矩形,
∴AB=CD,
∵M是BC的中点,
∴BM=MC,
∴DC•AE=DE•MC;
(3)解:∵M是BC中点,AD=BC=6
∴BM=$\frac{1}{2}$BC=3,
在Rt△ABM中,AB=4,
∴AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=5,
∵△ADE∽△MAB,
∴$\frac{AE}{BM}$=$\frac{AD}{AM}$,即$\frac{AE}{3}$=$\frac{6}{5}$,
∴AE=$\frac{18}{5}$,
∴EM=AM-AE=5-$\frac{18}{5}$=$\frac{7}{5}$.
点评 本题考查了相似三角形的判定与性质:有两组角对应相等的两三角形相似;相似三角形对应边的比相等.本题同时也考查了勾股定理和矩形的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.80 |
| 2 | 2 | 70 | 5.60 |
| 3 | 2 | 85 | 6.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
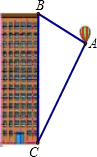 如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
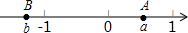 如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )
如图所示,数轴上A、B两点分别对应有理数a,b,则下列结论中正确的是( )| A. | a+b>0 | B. | ab>0 | C. | |a|-|b|>0 | D. | a-b>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com